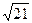题目内容
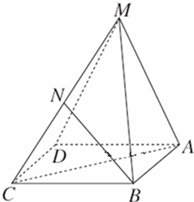
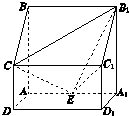
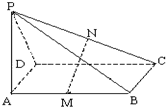
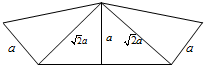
一个四棱锥S-ABCD的底面是边长为a的正方形,侧面展开图如图所示.SC为四棱锥中最长的侧棱,点E为AB的中点
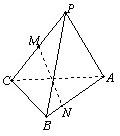
(1)画出四棱锥S-ABCD的示意图,求二面角E-SC-D的大小;
(2)求点D到平面SEC的距离.
(1)画出四棱锥S-ABCD的示意图,求二面角E-SC-D的大小;
(2)求点D到平面SEC的距离.

(12分)
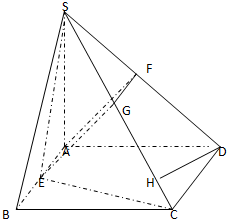
(1)四棱锥S-ABCD的示意图如图所示,…(2分)
分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG,
∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD,SA⊥CD,
又∵AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又∵SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD,
∴二面角E-SC-D的大小为90°.…(8分)
(2)作DH⊥SC于H,
∵面SEC⊥面SCD,∴DH⊥面SEC,
∴DH之长即为点D到面SEC的距离,
∵在Rt△SCD中,DH=
=
=
a,
答:点D到面SEC的距离为
a.…(12分)
(1)四棱锥S-ABCD的示意图如图所示,…(2分)
分别取SC、SD的中点G、F,连GE、GF、FA,
则GF∥EA,GF=EA,∴AF∥EG,
∵SA⊥AB,SA⊥AD,且AB、AD是面ABCD内的交线,
∴SA⊥底面ABCD,SA⊥CD,
又∵AD⊥CD,∴CD⊥面SAD,∴CD⊥AF,
又∵SA=AD,F是中点,∴AF⊥SD,
∴AF⊥面SCD,EG⊥面SCD,∴面SEC⊥面SCD,
∴二面角E-SC-D的大小为90°.…(8分)
(2)作DH⊥SC于H,
∵面SEC⊥面SCD,∴DH⊥面SEC,
∴DH之长即为点D到面SEC的距离,
∵在Rt△SCD中,DH=
| SD•DC |
| SC |
| ||
|
| ||
| 3 |
答:点D到面SEC的距离为
| ||
| 3 |


练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目