题目内容
16.函数y=$\sqrt{{x}^{2}-8x+20}$+$\sqrt{{x}^{2}+1}$的最小值是5,此时x=$\frac{4}{3}$.分析 把原函数解析式变成:y=$\sqrt{(x-4)^{2}+(0-2)^{2}}$+$\sqrt{{(x-0)}^{2}+(0-1)^{2}}$,问题转化为点(x,0)到点A(4,2)的距离与点(x,0)到点B(0,1)的距离的和,利用两点之间线段最短即可求y的最小值.
解答 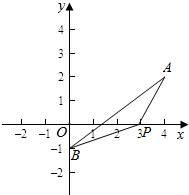 解:∵y=$\sqrt{{x}^{2}-8x+20}$+$\sqrt{{x}^{2}+1}$═$\sqrt{(x-4)^{2}+(0-2)^{2}}$+$\sqrt{(x-0)^{2}+(0+1)^{2}}$,
解:∵y=$\sqrt{{x}^{2}-8x+20}$+$\sqrt{{x}^{2}+1}$═$\sqrt{(x-4)^{2}+(0-2)^{2}}$+$\sqrt{(x-0)^{2}+(0+1)^{2}}$,
设P(x,0),A(4,2),B(0,-1);
∴y表示平面直角坐标系中:点P(x,0)到点A(4,2)的距离与点P(x,0)到点B(0,-1)的距离的和;
如图:
则|PA|+|PB|≥|AB|=$\sqrt{{4}^{2}+(-1-2)^{2}}$=$\sqrt{16+9}=\sqrt{25}=5$,
此时A,B,P三点共线,
即kAB=kBP,即$\frac{2+1}{4-0}$=$\frac{0+1}{x-0}$,
解得x=$\frac{4}{3}$,即P($\frac{4}{3}$,0),
即y=$\sqrt{{x}^{2}-8x+20}$+$\sqrt{{x}^{2}+1}$的最小值是5,此时x=$\frac{4}{3}$,
故答案为:5,$\frac{4}{3}$.
点评 本题主要考查函数最值的求解,以及平面直角坐标系中两点间的距离公式,将求函数的最小值转化成求距离和的最小值,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
8.已知函数f(x)=ax2+bx+c(a≠0),“-$\frac{b}{2a}$∈(p,q)”是“f(x)在(p,q)”上有最小值的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |