题目内容
 在正方体ABCD-A1B1C1D1中,M是CC1的中点,若点P在ABB1A1所在的平面上,满足∠PDB1=∠MDB1,则点P的轨迹是
在正方体ABCD-A1B1C1D1中,M是CC1的中点,若点P在ABB1A1所在的平面上,满足∠PDB1=∠MDB1,则点P的轨迹是
- A.圆
- B.椭圆
- C.双曲线
- D.抛物线
D
分析:由已知中点P在ABB1A1所在的平面上,满足∠PDB1=∠MDB1,我们根据直线与夹角相等的性质,我们可以判断DP的轨迹是一个以DB1为轴,以DP为母线的圆锥,由此可将问题转化为平面截圆锥得到圆锥曲线的形状判断问题,分析平面ABB1A1与母线及轴的关系,即可得到答案.
解答:若∠PDB1=∠MDB1,
则DP的轨迹应该是一个以DB1为轴,以DP为母线的圆锥,
平面ABB1A1是一个与母线DM平行的平面
又∵点P在ABB1A1所在的平面上,
∴P点的轨迹为一条抛物线
故选D
点评:本题考查的知识点是轨迹方程,圆锥曲线的形状,其中分析出DP的轨迹是一个以DB1为轴,以DP为母线的圆锥,将问题转化为平面截圆锥得到圆锥曲线的形状判断问题,是解答本题的关键.
分析:由已知中点P在ABB1A1所在的平面上,满足∠PDB1=∠MDB1,我们根据直线与夹角相等的性质,我们可以判断DP的轨迹是一个以DB1为轴,以DP为母线的圆锥,由此可将问题转化为平面截圆锥得到圆锥曲线的形状判断问题,分析平面ABB1A1与母线及轴的关系,即可得到答案.
解答:若∠PDB1=∠MDB1,
则DP的轨迹应该是一个以DB1为轴,以DP为母线的圆锥,
平面ABB1A1是一个与母线DM平行的平面
又∵点P在ABB1A1所在的平面上,
∴P点的轨迹为一条抛物线
故选D
点评:本题考查的知识点是轨迹方程,圆锥曲线的形状,其中分析出DP的轨迹是一个以DB1为轴,以DP为母线的圆锥,将问题转化为平面截圆锥得到圆锥曲线的形状判断问题,是解答本题的关键.

练习册系列答案
相关题目
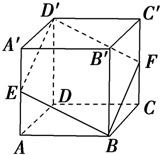 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则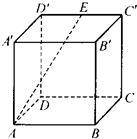
 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.  如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )
如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )