题目内容
7.下列函数中,既是奇函数,又是以π为周期的函数是( )| A. | y=x3tanx | B. | y=|sinx| | C. | y=-2sinxcosx | D. | y=tan|x| |
分析 由条件利用二倍角公式,三角函数的奇偶性和周期性,逐一判断各个选项是否满足条件,从而得出结论.
解答 解:由于y=x3tanx为偶函数,故排除A;由于y=|sinx|是偶函数,故排除B;
由于y=-2sinxcosx=-sin2x是奇函数,且还是以π为周期的函数,故满足条件;
由于y=tan|x|是偶函数,故排除D,
故选:C.
点评 本题主要考查二倍角公式,三角函数的奇偶性和周期性,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
2.已知cos(π-α)=-$\frac{5}{13}$且α是第四象限角,则sinα=( )
| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | ±$\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
19.有A、B、C、D、E共5人并排站一起,若A、B必须相邻,且B在A的右边,那么不同的站法有( )
| A. | 24种 | B. | 36种 | C. | 48种 | D. | 60种 |
16.在等差数列{an}中,a1+a19=10,则a10的值为( )
| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
17.化简2$\sqrt{1+sin10}$+$\sqrt{2+2cos10}$的结果是( )
| A. | 2sin5 | B. | 4cos5+2sin5 | C. | -4cos5-2sin5 | D. | -2sin5 |
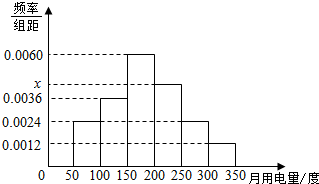 为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.
为调查我校学生的用电情况,学校后勤部门组织抽取了100间学生宿舍某月用电量调查,发现每间宿舍用电量都在50度到350度之间,其频率分布直方图如图所示.