题目内容
如图,正三棱柱ABC-A1B1C1中,AB=2,AA1=1,点P在平面BCC1B1内,PB1=PC1=
.
(1)求证:PA1⊥BC;
(2)求二面角C1-PA1-A.

| 2 |
(1)求证:PA1⊥BC;
(2)求二面角C1-PA1-A.

(1)证明:设B1C1的中点为D1,∵PB1=PC1,∴PD1⊥B1C1,
又∵△A1B1C1是正三角形,∴A1D1⊥B1C1,∴B1C1⊥平面PA1D1,
∴PA1⊥B1C1,
又∵BC∥B1C1,∴PA1⊥BC;
(2)∵平面PB1BCC1⊥平面A1B1C1,∴PD1⊥平面A1B1C1,
又∵AA1⊥平面A1B1C1,∴A,A1,P,D1四点共面,
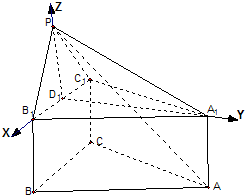
如图,以点D1为坐标原点,D1B1,D1A1,D1P所在直线分别为x轴,y轴,z轴,建立空间坐标系D1-xyz,
平面PAA1所在平面为坐标平面yOz,取平面PAA1的一个法向量
=(1,0,0)
 由PC1=PB1=
由PC1=PB1=
,B1C1=2得到PD1=1,
由A1B1=B1C1=C1A1=2得到A1D1=
,
点P的坐标为(0,0,1),点A1的坐标为(0,
,0),
点C1的坐标为(-1,0,0),
设平面PC1A1的法向量为
=(x,y,z),
则
•
=(x,y,z)•(0,
,-1)=0,所以z=
y
•
=(x,y,z)•(-1,0,-1)=0,所以x=-z,
令y=1,则
=(-
,1,
),
cos?
,
>=
=-
,
即所求二面角是arccos
.
又∵△A1B1C1是正三角形,∴A1D1⊥B1C1,∴B1C1⊥平面PA1D1,
∴PA1⊥B1C1,
又∵BC∥B1C1,∴PA1⊥BC;
(2)∵平面PB1BCC1⊥平面A1B1C1,∴PD1⊥平面A1B1C1,
又∵AA1⊥平面A1B1C1,∴A,A1,P,D1四点共面,
如图,以点D1为坐标原点,D1B1,D1A1,D1P所在直线分别为x轴,y轴,z轴,建立空间坐标系D1-xyz,
平面PAA1所在平面为坐标平面yOz,取平面PAA1的一个法向量
| m |
 由PC1=PB1=
由PC1=PB1=| 2 |
由A1B1=B1C1=C1A1=2得到A1D1=
| 3 |
点P的坐标为(0,0,1),点A1的坐标为(0,
| 3 |
点C1的坐标为(-1,0,0),
设平面PC1A1的法向量为
| n |
则
| n |
| PA1 |
| 3 |
| 3 |
| n |
| PC1 |
令y=1,则
| n |
| 3 |
| 3 |
cos?
| m |
| n |
-
| ||
|
| ||
| 7 |
即所求二面角是arccos
| ||
| 7 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 ,底面是边长为
,底面是边长为 的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( ).
的正三角形.若P为底面A1B1C1的中心,则PA与平面ABC所成角的大小为( ).


