题目内容

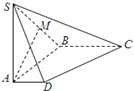
如图，三棱柱ABC-A′B′C′的所有棱长都相等，侧棱与底面垂直，M是侧棱BB′的中点，则二面角M-AC-B的大小为（　　）
A．30°B．45°C．60°D．75°
由已知中三棱柱ABC-A′B′C′的所有棱长都相等，侧棱与底面垂直，
可得三棱柱ABC-A′B′C′为直三棱柱
取AC的中点D，连接BD，MD，
则MD⊥AC，BD⊥AC
∴∠MDB即为二面角M-AC-B的平面角，
在Rt△MBD中，
∵M是侧棱BB′的中点
∴tan∠MDB=
MB
BD
=
3
3

故∠MDB=30°
即二面角M-AC-B的大小为30°
故选A
练习册系列答案
相关题目
已知△ABC是边长为l的等边三角形，D、E分别是AB、AC边上的点，AD = AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到三棱锥A－BCF，其中．
(1)证明：DE∥平面BCF；
(2)证明：CF⊥平面ABF；
(3)当时，求三棱锥F－DEG的体积V．
如图，在正三棱柱ABC－A1B1C1中，点D为棱AB的中点，BC＝1，AA1＝.
(1)求证：BC1∥平面A1CD；
(2)求三棱锥D－A1B1C的体积.
如图，四棱锥中，底面ABCD是菱形，SA=SD=
39
，AD=2
3
，且S-AD-B大小为120°，∠DAB=60°．
（1）求异面直线SA与BD所成角的正切值；
（2）求证：二面角A-SD-C的大小．
如图，在四棱锥S-ABCD中，底面ABCD是直角梯形，侧棱SA⊥底面ABCD，AB垂直于AD和BC，SA=AB=BC=2，AD=1，M是棱SB的中点．
（Ⅰ）求证：AM∥面SCD；
（Ⅱ）求面SCD与面SAB所成二面角的余弦值．
在三棱柱ABC-A1B1C1中，∠BCA=90°，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D，又知BA1⊥AC1．
（1）求证：AC1⊥平面A1BC；
（2）求二面角A1-BC-A的大小；
（3）求CC1到平面A1AB的距离．
如图，梯形ABCD中，AD∥BC，∠ABC=
π
2
，AB=a，AD=3a，∠ADC=arcsin
5
5
，PA⊥面ABCD，PA=a．求：
（1）二面角P-CD-A的大小（用反三角函数表示）；
（2）点A到平面PBC的距离．
如图，正三棱柱ABC-A1B1C1中，AB=2，AA1=1，点P在平面BCC1B1内，PB1=PC1=
2
．
（1）求证：PA1⊥BC；
（2）求二面角C1-PA1-A．
如图，矩形ABCD中，AB=a，AD=b，过点D作DE⊥AC于E，交直线AB于F．现将△ACD沿对角线AC折起到△PAC的位置，使二面角P-AC-B的大小为60°．过P作PH⊥EF于H．
（I）求证：PH⊥平面ABC；
（Ⅱ）若a=
2
b，求直线DP与平面PBC所成角的大小；
（Ⅲ）若a+b=2，求四面体P-ABC体积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网