题目内容
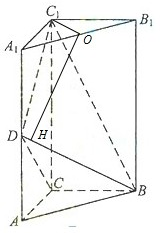
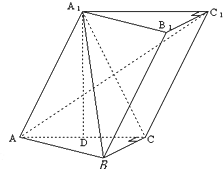
如图,直三棱柱ABC-A1B1C1中,AC=BC=
AA1,D是棱AA1的中点,DC1⊥BD
(1)证明:DC1⊥BC
(2)求二面角A1-BD-C1的大小.

| 1 |
| 2 |
(1)证明:DC1⊥BC
(2)求二面角A1-BD-C1的大小.

(1)证明:在Rt△DAC中,AD=AC,∴∠ADC=45°
同理:∠A1DC1=45°,∴∠CDC1=90°
∴DC1⊥DC,DC1⊥BD
∵DC∩BD=D
∴DC1⊥面BCD
∵BC?面BCD
∴DC1⊥BC
(2)∵DC1⊥BC,CC1⊥BC,DC1∩CC1=C1,∴BC⊥面ACC1A1,
∵AC?面ACC1A1,∴BC⊥AC
取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,OH
∵A1C1=B1C1,∴C1O⊥A1B1,
∵面A1B1C1⊥面A1BD,面A1B1C1∩面A1BD=A1B1,
∴C1O⊥面A1BD
而BD?面A1BD
∴BD⊥C1O,
∵OH⊥BD,C1O∩OH=O,
∴BD⊥面C1OH∴C1H⊥BD,∴点H与点D重合且∠C1DO是二面角A1-BD-C1的平面角
设AC=a,则C1O=
,C1D=
a=2C1O,
∴sin∠C1DO=
∴∠C1DO=30°
即二面角A1-BD-C1的大小为30°
同理:∠A1DC1=45°,∴∠CDC1=90°
∴DC1⊥DC,DC1⊥BD
∵DC∩BD=D
∴DC1⊥面BCD
∵BC?面BCD
∴DC1⊥BC
(2)∵DC1⊥BC,CC1⊥BC,DC1∩CC1=C1,∴BC⊥面ACC1A1,
∵AC?面ACC1A1,∴BC⊥AC
取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,OH
∵A1C1=B1C1,∴C1O⊥A1B1,
∵面A1B1C1⊥面A1BD,面A1B1C1∩面A1BD=A1B1,
∴C1O⊥面A1BD
而BD?面A1BD
∴BD⊥C1O,
∵OH⊥BD,C1O∩OH=O,
∴BD⊥面C1OH∴C1H⊥BD,∴点H与点D重合且∠C1DO是二面角A1-BD-C1的平面角
设AC=a,则C1O=
| ||
| 2 |
| 2 |
∴sin∠C1DO=
| 1 |
| 2 |
∴∠C1DO=30°
即二面角A1-BD-C1的大小为30°


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.




 是
是 所在平面
所在平面 外一点,若
外一点,若 ,则
,则
 ;
; ;
; .
.