题目内容
在数列{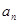 }中,
}中,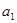 =1,
=1,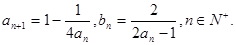 (1)求
(1)求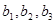
写出数列{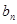 }的通项公式(不要求证明);(2)求证:对于任意的n
}的通项公式(不要求证明);(2)求证:对于任意的n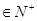 都有
都有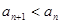 ;(3)设
;(3)设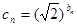 证明:数列{
证明:数列{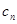 }不存在成等差数列的三项。
}不存在成等差数列的三项。
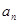 }中,
}中,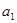 =1,
=1,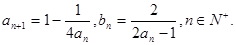 (1)求
(1)求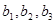
写出数列{
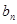 }的通项公式(不要求证明);(2)求证:对于任意的n
}的通项公式(不要求证明);(2)求证:对于任意的n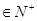 都有
都有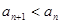 ;(3)设
;(3)设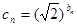 证明:数列{
证明:数列{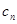 }不存在成等差数列的三项。
}不存在成等差数列的三项。(1)
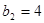
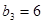
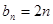 ; (2)
; (2)
 ;(3)见解析.
;(3)见解析.

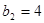
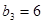
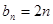 ; (2)
; (2)
 ;(3)见解析.
;(3)见解析.第一问中利用递推关系可知,数列的前几项,
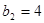
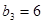 并猜想
并猜想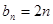
第二问中,利用定义法作差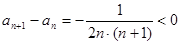 判定单调性即可。
判定单调性即可。
第三问中假设存在三项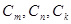 成等差数列。(
成等差数列。(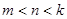 )
)
则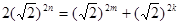
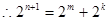
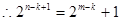
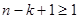 ,
, 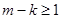 的正整数
的正整数 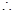 左边为偶数,右边为奇数
左边为偶数,右边为奇数
矛盾;假设错误命题成立
解:(1)
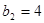
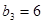
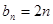 …………………………4分
…………………………4分
(2)
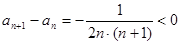

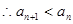 ………………8分
………………8分
(3)假设存在三项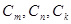 成等差数列。(
成等差数列。(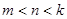 )
)
则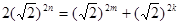
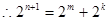
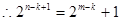
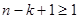 ,
, 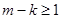 的正整数
的正整数 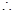 左边为偶数,右边为奇数
左边为偶数,右边为奇数
矛盾;假设错误命题成立……………………14分

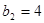
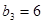 并猜想
并猜想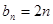
第二问中,利用定义法作差
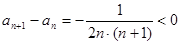 判定单调性即可。
判定单调性即可。第三问中假设存在三项
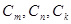 成等差数列。(
成等差数列。(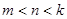 )
)则
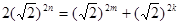
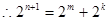
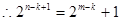
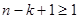 ,
, 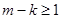 的正整数
的正整数 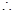 左边为偶数,右边为奇数
左边为偶数,右边为奇数矛盾;假设错误命题成立
解:(1)

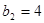
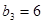
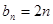 …………………………4分
…………………………4分(2)

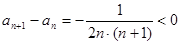

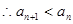 ………………8分
………………8分(3)假设存在三项
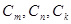 成等差数列。(
成等差数列。(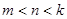 )
)则
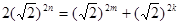
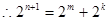
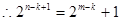
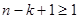 ,
, 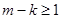 的正整数
的正整数 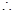 左边为偶数,右边为奇数
左边为偶数,右边为奇数矛盾;假设错误命题成立……………………14分

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
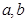 ,可按规则
,可按规则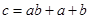 扩充为一个新数
扩充为一个新数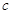 ,在
,在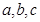 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.若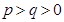 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为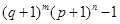 (
(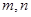 为正整数),则
为正整数),则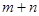 的值为 ▲ .
的值为 ▲ .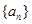 是首项为0的递增数列,
是首项为0的递增数列,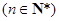 ,
,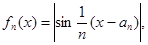
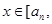
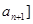 满足:对于任意的
满足:对于任意的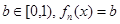 总有两个不同的根. (Ⅰ)试写出
总有两个不同的根. (Ⅰ)试写出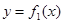 ,并求出
,并求出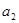 ;
; 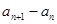 ,并求出
,并求出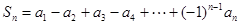 ,求
,求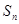 .
.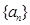 的前n项和为
的前n项和为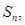 若
若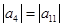 ,且公差
,且公差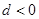 ,则当
,则当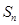 取最大值时,
取最大值时, 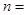 __________.
__________.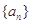 满足:所有的奇数项
满足:所有的奇数项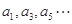 构成以1为首项,1为公差的等差数列;所有的偶数项
构成以1为首项,1为公差的等差数列;所有的偶数项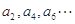 构成以2为首项,3为公差的等差数列,则
构成以2为首项,3为公差的等差数列,则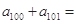 ( )
( )
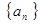 定义如下:
定义如下: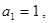
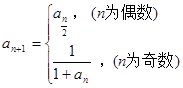 , 则前
, 则前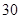 项中使
项中使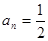 的项的个数是( ▲ )
的项的个数是( ▲ )
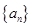 中,
中,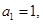 前
前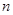 项和为
项和为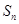 ,且点
,且点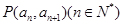 在直线
在直线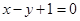 上,则
上,则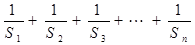 =( )
=( )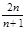

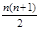
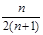
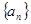 是各项正的等比数列,且
是各项正的等比数列,且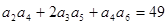 ,则
,则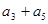 =
= 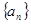 中,
中,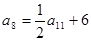 ,则数列
,则数列 项和
项和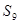 等于( )
等于( )


