题目内容
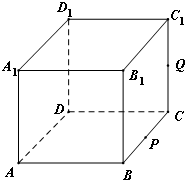
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是______(写出所有正确命题的编号).
①当0<CQ<
时,S为四边形
②当CQ=
时,S为等腰梯形
③当CQ=
时,S与C1D1的交点R满足C1R=
④当
<CQ<1时,S为六边形
⑤当CQ=1时,S的面积为
.
①当0<CQ<
| 1 |
| 2 |
②当CQ=
| 1 |
| 2 |
③当CQ=
| 3 |
| 4 |
| 1 |
| 3 |
④当
| 3 |
| 4 |
⑤当CQ=1时,S的面积为
| ||
| 2 |

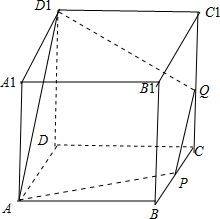
如图
当CQ=
时,即Q为CC1中点,此时可得PQ∥AD1,AP=QD1=
=
,
故可得截面APQD1为等腰梯形,故②正确;
由上图当点Q向C移动时,满足0<CQ<
,只需在DD1上取点M满足AM∥PQ,
即可得截面为四边形APQM,故①正确;
③当CQ=
时,如图,
延长DD1至N,使D1N=
,连接AN交A1D1于S,连接NQ交C1D1于R,连接SR,
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=
,故正确;
④由③可知当
<CQ<1时,只需点Q上移即可,此时的截面形状仍然上图所示的APQRS,显然为五边形,故错误;
⑤当CQ=1时,Q与C1重合,取A1D1的中点F,连接AF,可证PC1∥AF,且PC1=AF,
可知截面为APC1F为菱形,故其面积为
AC1•PF=
•
•
=
,故正确.
故答案为:①②③⑤
当CQ=
| 1 |
| 2 |
12+(
|
| ||
| 2 |
故可得截面APQD1为等腰梯形,故②正确;
由上图当点Q向C移动时,满足0<CQ<
| 1 |
| 2 |
即可得截面为四边形APQM,故①正确;
③当CQ=
| 3 |
| 4 |

延长DD1至N,使D1N=
| 1 |
| 2 |
可证AN∥PQ,由△NRD1∽△QRC1,可得C1R:D1R=C1Q:D1N=1:2,故可得C1R=
| 1 |
| 3 |
④由③可知当
| 3 |
| 4 |
⑤当CQ=1时,Q与C1重合,取A1D1的中点F,连接AF,可证PC1∥AF,且PC1=AF,
可知截面为APC1F为菱形,故其面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
故答案为:①②③⑤


练习册系列答案
相关题目