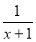Question

设f(x)＝x3＋ax2＋bx＋1的导数f′(x)满足f′(1)＝

2a，f′(2)＝－b，其中a，b∈R.

①求曲线y＝f(x)在点(1，f(1))处的切线方程；②设g(x)＝f′(x)e－x，求g(x)的极值．

 

Answer 1

①6x＋2y－1＝0. ②极小值g(0)＝－3；极大值g(3)＝15e－3

【解析】①f′(x)＝3x2＋2ax＋b.

∵f′(1)＝2a，f′(2)＝－b，

∴3＋2a＋b＝2a,12＋4a＋b＝－b.∴a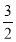＝－，b＝－3.

∴f(x)＝x3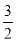－x2－3x＋1.从而f(1)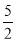＝－.又f′(1)＝2a＝－3，

∴f(x)在点(1，f(1))处的切线方程为y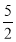＋＝－3(x－1)，即6x＋2y－1＝0.

②g(x)＝(3x2－3x－3)e－x，

∴g′(x)＝(6x－3)e－x－

e－x(3x2－3x－3)＝(－3x2＋9x)e－x.

令g′(x)＝0得x＝0或x＝3.

当x∈(－∞，0)时，g′(x)<0；

当x∈(0,3)时，g′(x)>0；

当x∈(3，＋∞)时，g′(x)<0.

∴g(x)在(－∞，0)上是减函数，在(0,3)上是增函数，在(3，＋∞)上是减函数．

当x＝0时，g(x)取得极小值g(0)＝－3；当x＝3时，g(x)取得极大值g(3)＝15e－3