题目内容
(本题满分12分)
(Ⅰ)从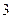 名男生和
名男生和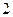 名女生中任选
名女生中任选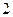 人去参加培训,用
人去参加培训,用 表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件
表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件 的对立事件,并求事件
的对立事件,并求事件 的概率;
的概率;
(Ⅱ)函数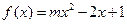 ,那么任意
,那么任意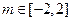 ,使函数
,使函数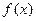 在实数集上有零根的概率.
在实数集上有零根的概率.
(Ⅰ)从
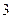 名男生和
名男生和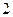 名女生中任选
名女生中任选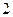 人去参加培训,用
人去参加培训,用 表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件
表示事件“其中至少有一名女生”,写出从中选取两人的所有可能取法和事件 的对立事件,并求事件
的对立事件,并求事件 的概率;
的概率;(Ⅱ)函数
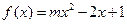 ,那么任意
,那么任意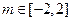 ,使函数
,使函数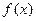 在实数集上有零根的概率.
在实数集上有零根的概率.(1)

(2)

解: (Ⅰ)设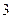 位男生分别为
位男生分别为 ;两位女生分别为
;两位女生分别为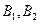
事件 表示“其中至少有一名女生”,则其对立事件
表示“其中至少有一名女生”,则其对立事件 为没有女生参加
为没有女生参加
从以上 位同学任选两位同学,情况列举如下:
位同学任选两位同学,情况列举如下: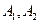 ,
, ,
, 
 ,
,  ,
,  ,
, 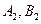 ,
,  ,
,  ,
, 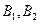
共
 种选法,每种选法出现的可能性相同,其中没有女生参加的情形只有
种选法,每种选法出现的可能性相同,其中没有女生参加的情形只有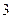 种,
种,
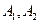 ,
,  ,
, 
由等可能性事件的概率可得:
由对立事件概率性质,可得: ………………………8分
………………………8分
(Ⅱ) 设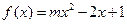 在实数集上有零根为事件
在实数集上有零根为事件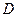 ,
,
事件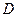 发生当且仅当:
发生当且仅当:
即:
而 为
为 中的任意值,
中的任意值,
∴ 中的所有实数都可以满足使
中的所有实数都可以满足使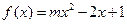 在实数集上有零根
在实数集上有零根
根据几何概率, ……………………………………………12分
……………………………………………12分
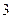 位男生分别为
位男生分别为 ;两位女生分别为
;两位女生分别为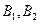
事件
 表示“其中至少有一名女生”,则其对立事件
表示“其中至少有一名女生”,则其对立事件 为没有女生参加
为没有女生参加从以上
 位同学任选两位同学,情况列举如下:
位同学任选两位同学,情况列举如下: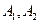 ,
, ,
, 
 ,
,  ,
,  ,
, 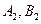 ,
,  ,
,  ,
, 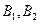
共

 种选法,每种选法出现的可能性相同,其中没有女生参加的情形只有
种选法,每种选法出现的可能性相同,其中没有女生参加的情形只有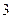 种,
种,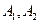 ,
,  ,
, 
由等可能性事件的概率可得:

由对立事件概率性质,可得:
 ………………………8分
………………………8分(Ⅱ) 设
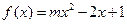 在实数集上有零根为事件
在实数集上有零根为事件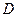 ,
,事件
 发生当且仅当:
发生当且仅当:
即:

而
 为
为 中的任意值,
中的任意值,
∴
 中的所有实数都可以满足使
中的所有实数都可以满足使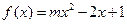 在实数集上有零根
在实数集上有零根根据几何概率,
 ……………………………………………12分
……………………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 4、5组中用分层抽样法抽取6名学生进入第二轮面试,问第3、4、5组每组各抽取多少名学生进入第二轮面试?
4、5组中用分层抽样法抽取6名学生进入第二轮面试,问第3、4、5组每组各抽取多少名学生进入第二轮面试?

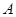 发生的概率为
发生的概率为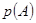 ,则
,则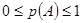
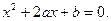 (1)若
(1)若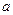 是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若
是从0,1,2,3四个数中任取一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率。(2)若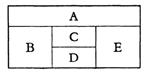
 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率; 求
求 学期望E
学期望E