题目内容
是否存在实数a,使得函数y=sin2x+a·cos x+a-在闭区间上的最大值是1?若存在,求出对应的a值;若不存在,试说明理由
y=1-cos2x+acos x+a-
=-2++a-.
当0≤x≤时,0≤cos x≤1.
若>1时,即a>2,则当cos x=1时,
ymax=a+a-=1⇒a=<2(舍去),
若0≤≤1,即0≤a≤2,则当cos x=时,
ymax=+a-=1⇒a=或a=-4<0(舍去).
若<0,即a<0,则当cos x=0时,
ymax=a-=1⇒a=>0(舍去).
综合上述知,存在a=符合题设.
=-2++a-.
当0≤x≤时,0≤cos x≤1.
若>1时,即a>2,则当cos x=1时,
ymax=a+a-=1⇒a=<2(舍去),
若0≤≤1,即0≤a≤2,则当cos x=时,
ymax=+a-=1⇒a=或a=-4<0(舍去).
若<0,即a<0,则当cos x=0时,
ymax=a-=1⇒a=>0(舍去).
综合上述知,存在a=符合题设.
略

练习册系列答案
相关题目
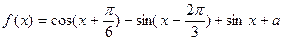 的最大值为
的最大值为 .
.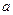 的值;
的值; 成立的
成立的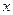 的取值范围.
的取值范围. 的图象的一部分,A是图象与x轴的一个交点,B、C分别是图象上的一个最高点和一个最低点,且AB⊥AC,则ω的值为 ( )
的图象的一部分,A是图象与x轴的一个交点,B、C分别是图象上的一个最高点和一个最低点,且AB⊥AC,则ω的值为 ( ) D.
D.

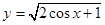 的定义域是 ( )
的定义域是 ( )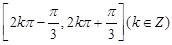
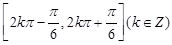
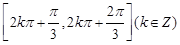
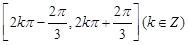

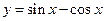 的图象可由
的图象可由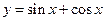 的图像向右平移( )
的图像向右平移( )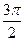 个单位
个单位
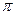 个单位
个单位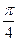 个单位
个单位 个单位
个单位