题目内容
已知函数y=|cosx+sinx|.
(1)画出函数在x∈[-,]的简图;
(2)写出函数的最小正周期和单调递增区间;试问:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
(1)画出函数在x∈[-,]的简图;
(2)写出函数的最小正周期和单调递增区间;试问:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状.
(1)∵y=|cosx+sinx|=,
当x∈时,其图象如图所示.
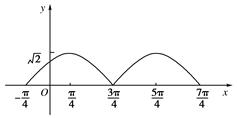
(2)函数的最小正周期是π,其单调递增区间是
(k∈Z).
由图象可以看出,当x=kπ+(k∈Z)时,该函数的最大值是.
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.由y2=1,
得|cosx+sinx|2=1
⇒1+sin2x=1.
∴sin2x=0,∴2x=π,x=,
故△ABC为直角三角形.
当x∈时,其图象如图所示.

(2)函数的最小正周期是π,其单调递增区间是
(k∈Z).
由图象可以看出,当x=kπ+(k∈Z)时,该函数的最大值是.
(3)若x是△ABC的一个内角,则有0<x<π,
∴0<2x<2π.由y2=1,
得|cosx+sinx|2=1
⇒1+sin2x=1.
∴sin2x=0,∴2x=π,x=,
故△ABC为直角三角形.
略

练习册系列答案
相关题目
 =
=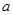 tan
tan -
-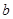 sin
sin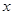 +4(其中
+4(其中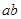
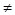 0),如果
0),如果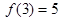 ,则
,则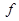 (2010
(2010 -3)的值为 ( )
-3)的值为 ( )  ,求
,求 的定义域和值域;
的定义域和值域;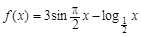 的图象与x轴交点的个数是
的图象与x轴交点的个数是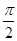 的是( )
的是( )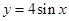
 的定义域为 .
的定义域为 . 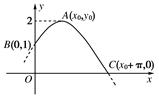
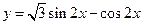 的图像,只需要将函数
的图像,只需要将函数 的图像 ( ).
的图像 ( ).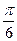 个单位
个单位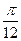 个单位
个单位