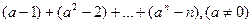题目内容
在等比数列{an}中,已知a2=2,a3=4.
(1)求数列{an}的通项an;
(2)设bn=an+1,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项an;
(2)设bn=an+1,求数列{bn}的前n项和Tn.
(1)由a2=2,a3=4,得q=
=2,∴a1=
=1,从而an=2n-1.
(2)∵bn=an+1=2n-1+1,
∴Tn=
+n=2n-1+n.
| a3 |
| a2 |
| a2 |
| q |
(2)∵bn=an+1=2n-1+1,
∴Tn=
| 1-2n |
| 1-2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目