题目内容
已知函数f(x)=ex-x(e为自然对数的底数).
(1)求f(x)的最小值;
(2)若不等式f(x)>ax的解集为P,若M={x|
≤x≤
},且M∩P≠φ,求实数a的取值范围.
(1)求f(x)的最小值;
(2)若不等式f(x)>ax的解集为P,若M={x|
| 1 |
| 2 |
| 3 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)先求导数,然后根据函数的单调性研究函数的极值点,连续函数f(x)在区间(a,b)内只有一个极值,那么极小值就是最小值;
(2)根据不等式f(x)>ax的解集为P,且{x|
≤x≤2}且两个集合的交集不是空集,可转化成,对任意的x∈[
,2],不等式f(x)>ax有解,将(1+a)x<ex变形为 a<
-1,令g(x)=
-1,利用导数研究g(x)的最大值,使a小于最大值即可.
(2)根据不等式f(x)>ax的解集为P,且{x|
| 1 |
| 2 |
| 1 |
| 2 |
| ex |
| x |
| ex |
| x |
解答:
解:(1)f′(x)=ex-1,由f′(x)=0得x=0,
当x>0时f′(x)>0,
当x<0时f′(x)<0,
∴f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减,
∴f(x)max=f(0)=1.
(2)∵M∩P≠∅,∴f(x)>ax在区间[
,
]上有解,
由f(x)>ax,得ex-x>ax,即a<
-1在[
,
]上有解,
令g(x)=
-1,x∈[
,
],
∵g′(x)=
,
∴g(x)在[
,1]上单调递减,[1,
]上单调递增,
又g(
)=2
-1,g(
)=
e
-1,且g(
)>g(
),
g(x)max=g(
)=2
-1,
∴a<2
-1.
当x>0时f′(x)>0,
当x<0时f′(x)<0,
∴f(x)在(0,+∞)上单调递增,在(-∞,0)上单调递减,
∴f(x)max=f(0)=1.
(2)∵M∩P≠∅,∴f(x)>ax在区间[
| 1 |
| 2 |
| 3 |
| 2 |
由f(x)>ax,得ex-x>ax,即a<
| ex |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
令g(x)=
| ex |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
∵g′(x)=
| ex(x-1) |
| x2 |
∴g(x)在[
| 1 |
| 2 |
| 3 |
| 2 |
又g(
| 1 |
| 2 |
| e |
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
g(x)max=g(
| 1 |
| 2 |
| e |
∴a<2
| e |
点评:本题主要考查了利用导数求闭区间上函数的最值,一般有解求参数问题常常将参数进行分离,转化成研究已知函数在某个区间上的最值问题,属于中档题.

练习册系列答案
相关题目
下列命题中正确的是( )
| A、三角形的内角是第一象限角或第二象限角 | ||
| B、第一象限角是锐角 | ||
| C、第一象限角不是锐角 | ||
D、角α是第四象限角则有2kπ-
|
如图,汉若塔问题是指有3根杆子A、B、C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的上面.把B杆上的5个碟子全部移到A杆上,最少需要移动( )


| A、31次 | B、32次 |
| C、33次 | D、35次 |
设抛物线的顶点在原点,准线方程为y=2,则抛物线的方程是( )
| A、x2=8y |
| B、x2=-8y |
| C、y2=-8x |
| D、y2=-8x |
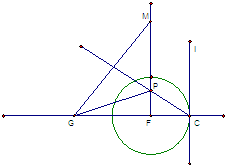 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
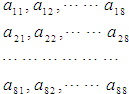 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=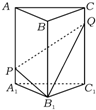 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为