题目内容
某发电厂在节能减排的科研活动中,对热能与电能的转化和燃煤每分钟的添加量之间的关系进行科学研究,对该厂A号机组的跟踪调研中发现,若该机组每分钟燃煤的添加量设计标准为a吨,在正常状态下,通过自动传输带给该机组每分钟添加燃煤x吨,理论上可以生产电能x3-x+10千瓦,而由于实际添加量x与设计标准a存在误差,实际上会导致电能损耗2|x-a|千瓦,最终生产的电能为f(x)千瓦.
(1)试写出f(x)关于x的函数表达式,并求出f(x)的单调增区间;
(2)该科研小组决定调整设计标准a,控制添加量x∈[
,
](单位:吨),实现对最终生产的电能f(x)的有效控制的科学实验,若某次试验中a∈[
,1](单位:吨),用电高峰期间,要求该厂的输出电能为每分钟不低于9千瓦,否则将供电不正常,试问这次实验能否实现这个目标?
(1)试写出f(x)关于x的函数表达式,并求出f(x)的单调增区间;
(2)该科研小组决定调整设计标准a,控制添加量x∈[
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
考点:函数模型的选择与应用
专题:计算题,应用题,函数的性质及应用
分析:(1)由题意,f(x)=x3-x+10-2|x-a|=
,从而由导数写出函数的单调区间;
(2)当
≤a<1时,f(x)在[
,a),[1,
]上单调递增,在(a,1)上单调递减,从而化恒成立问题为最值问题.
|
(2)当
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)由题意,
f(x)=x3-x+10-2|x-a|
=
,
∵当0<x<a时,f′(x)=3x2+1>0,
∴f(x)在(0,a)上单调递增,
当x≥a时,f′(x)=3x2-3,
故当0<a<1时,f(x)在[1,+∞)上单调递增,
当a≥1时,f(x)在[a,+∞)上单调递增,
故当0<a<1时,f(x)单调增区间为(0,a),[1,+∞);
当a≥1时,f(x)单调增区间为R;
(2)当
≤a<1时,f(x)在[
,a),[1,
]上单调递增,在(a,1)上单调递减,
且f(
)=
+
+10-2a有可能小于9,
故这次实验不能实现这个目标.
f(x)=x3-x+10-2|x-a|
=
|
∵当0<x<a时,f′(x)=3x2+1>0,
∴f(x)在(0,a)上单调递增,
当x≥a时,f′(x)=3x2-3,
故当0<a<1时,f(x)在[1,+∞)上单调递增,
当a≥1时,f(x)在[a,+∞)上单调递增,
故当0<a<1时,f(x)单调增区间为(0,a),[1,+∞);
当a≥1时,f(x)单调增区间为R;
(2)当
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
且f(
| 1 |
| 2 |
| 1 |
| 8 |
| 1 |
| 2 |
故这次实验不能实现这个目标.
点评:本题考查了学生将实际问题转化为数学问题的能力及分段函数的最值问题,属于中档题.

练习册系列答案
相关题目
解下列不等式:
(1)|4x-3|<21;
(2)|
+2|≥
;
(3)
>
;
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
(1)|4x-3|<21;
(2)|
| x-1 |
| 2 |
| 3 |
| 4 |
(3)
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
在四边形ABCD中,若
=
+
,则四边形ABCD的形状一定是( )
| AC |
| AB |
| AD |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
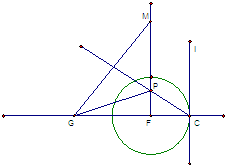 如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
如图,直线λ与半径为1的圆F相切于C.动点P到直线λ的距离为d,已知
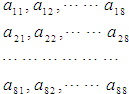 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=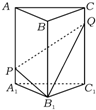 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为