题目内容
 如图,在椭圆
如图,在椭圆| x2 |
| a2 |
| y2 |
| 8 |
(Ⅰ)求a的值;
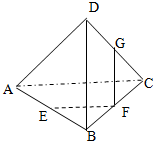
(Ⅱ)若四边形EBCF2为平行四边形,求点C的坐标;
(Ⅲ)当S△AF1O=S△CEO时,求直线AC的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知得a=3c,b2=8,由此能求出a=3.
(II)由a=3,B(-3,0),F1(-1,0),得F1为BF2的中点,由已知C,E关于F1(-1,0)对称,设C(x0,y0),则-2-x0=0,由此能求出点C的坐标.
(III)依题意直线AC的斜率存在,设直线AC:y=k(x+1),A(x1,y1),B(x2,y2),由
,得(8+9k2)x2+18k2x+9(k2-8)=0,由此能求出直线AC的方程.
(II)由a=3,B(-3,0),F1(-1,0),得F1为BF2的中点,由已知C,E关于F1(-1,0)对称,设C(x0,y0),则-2-x0=0,由此能求出点C的坐标.
(III)依题意直线AC的斜率存在,设直线AC:y=k(x+1),A(x1,y1),B(x2,y2),由
|
解答:
(本小题满分13分)
解:(I)∵F1,F2三等份BD,
∴|F1F2|=
|BD|,即2c=
•2a,a=3c…(1分)
∵a2=b2+c2,b2=8,∴a2=9,
∵a>0,∴a=3.
(II)由(I)知a=3,B(-3,0),F1(-1,0),
∴F1为BF2的中点,
∵四边形EBCF2为平行四边形,
∴C,E关于F1(-1,0)对称,
设C(x0,y0),则-2-x0=0,解得x0=-2,
∵
+
=1,∴
+
=1,
解得y0=±
,
∴C(-2,
)或C(-2,
).
(III)依题意直线AC的斜率存在,
设直线AC:y=k(x+1),A(x1,y1),B(x2,y2),
由
,得(8+9k2)x2+18k2x+9(k2-8)=0,
x1+x2=-
,x1x2=
,
∵S△AF1O=S△CEO,
∴
|AF1|h=
|CE|h,(h表示原点O到直线AC的距离),
∴
|x1+1|=
|x2|,即|x1+1|=|x2|,
∴x2+x1=-1,…(10分)
,
∴k2=
,∴k=±
,,∴k=
,
∴直线AC的方程为y=
(x+1).
解:(I)∵F1,F2三等份BD,
∴|F1F2|=
| 1 |
| 3 |
| 1 |
| 3 |
∵a2=b2+c2,b2=8,∴a2=9,
∵a>0,∴a=3.
(II)由(I)知a=3,B(-3,0),F1(-1,0),
∴F1为BF2的中点,
∵四边形EBCF2为平行四边形,
∴C,E关于F1(-1,0)对称,
设C(x0,y0),则-2-x0=0,解得x0=-2,
∵
| ||
| 9 |
| ||
| 8 |
| 4 |
| 9 |
| y02 |
| 8 |
解得y0=±
2
| ||
| 3 |
∴C(-2,
2
| ||
| 3 |
2
| ||
| 3 |
(III)依题意直线AC的斜率存在,
设直线AC:y=k(x+1),A(x1,y1),B(x2,y2),
由
|
x1+x2=-
| 18k2 |
| 8+9k2 |
| 9(k2-8) |
| 8+9k2 |
∵S△AF1O=S△CEO,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1+k2 |
| 1+k2 |
∴x2+x1=-1,…(10分)
|
∴k2=
| 8 |
| 9 |
2
| ||
| 3 |
2
| ||
| 3 |
∴直线AC的方程为y=
2
| ||
| 3 |
点评:本题考查a的值的求法,考查点C的坐标的求法,考查直线AC的方程的求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,汉若塔问题是指有3根杆子A、B、C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的上面.把B杆上的5个碟子全部移到A杆上,最少需要移动( )


| A、31次 | B、32次 |
| C、33次 | D、35次 |
设抛物线的顶点在原点,准线方程为y=2,则抛物线的方程是( )
| A、x2=8y |
| B、x2=-8y |
| C、y2=-8x |
| D、y2=-8x |
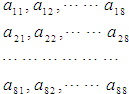 64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=
64个正数排成8行8列,如图所示:在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数.已知每一行中的数依次都成等差数列,而每一列中的数依次都成等比数列(每列公比q都相等)且a11=