题目内容
设 ,函数
,函数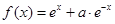 的导函数
的导函数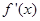 是奇函数,若曲线
是奇函数,若曲线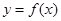 的一条切线的斜率是
的一条切线的斜率是 ,则切点的横坐标为( )
,则切点的横坐标为( )
A.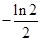 | B.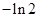 | C.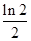 | D.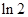 |
D
解析试题分析:由题意可得,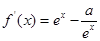 是奇函数,∴
是奇函数,∴ ,∴a=1,
,∴a=1,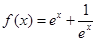 ,
,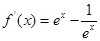 ,∵曲线y=f(x)在(x,y)的一条切线的斜率是
,∵曲线y=f(x)在(x,y)的一条切线的斜率是 ,∴
,∴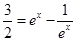 ,解方程可得ex=2,
,解方程可得ex=2,
∴x=ln2.
考点:1、函数的奇偶性;2、导数的运算.

练习册系列答案
相关题目
(5分)(2011•陕西)方程|x|=cosx在(﹣∞,+∞)内( )
| A.没有根 | B.有且仅有一个根 | C.有且仅有两个根 | D.有无穷多个根 |
下图揭示了一个由区间 到实数集
到实数集 上的对应过程:区间
上的对应过程:区间 内的任意实数
内的任意实数 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 围成一个圆,使两端
围成一个圆,使两端 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点
轴上,点 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线 与
与 轴交于点
轴交于点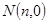 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( )
 ;
;  是偶函数;
是偶函数;  在其定义域上是增函数;
在其定义域上是增函数;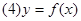 的图像关于点
的图像关于点 对称.
对称.
| A.(1)(3)(4). | B.(1)(2)(3). | C.(1)(2)(4). | D.(1)(2)(3)(4). |
已知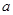 是函数
是函数 的零点,
的零点,
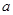 ,则
,则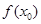 的值满足( )
的值满足( )
A.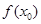 =0 =0 | B.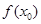 >0 >0 |
C.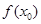 <0 <0 | D.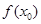 的符号不确定 的符号不确定 |
(2014·宜昌模拟)若定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在区间[0,1]上单调递减,则( )
A.f(2)<f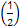 <f(1) <f(1) | B.f(1)<f(2)<f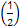 |
C.f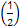 <f(2)<f(1) <f(2)<f(1) | D.f(1)<f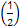 <f(2) <f(2) |
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则(x-3)f(x-3)<0的解集是( )
| A.(-3,0)或(3,+∞) | B.(-3,3) |
| C.(0,3) | D.(0,3)或(3,6) |
已知函数f(x)=ax3-3ax+3a-5至少有两个零点,则实数a的取值范围是( )
| A.[1,4] | B.[2,5] | C.[1,5] | D.[-5,-1] |
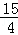
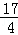
 ,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )