题目内容
15.设锐角△ABC的三个内角A、B、C的对边长分别为a、b、c,若sinA=$\frac{4}{5}$,∠B=$\frac{π}{4}$.(1)求cosA及sinC的值:
(2)若b=2$\sqrt{2}$,求a及△ABC的面积S.
分析 (1)利用同角三角函数关系式可求cosA的值,由sinC=sin(A+B),根据两角和的正弦函数公式即可求值.
(2)由正弦定理可得a=$\frac{bsinA}{sinB}$的值,根据三角形面积公式即可求△ABC的面积S.
解答 解:(1)∵锐角△ABC的三个内角A、B、C的对边长分别为a、b、c,若sinA=$\frac{4}{5}$,∠B=$\frac{π}{4}$.
∴cosA=$\sqrt{1-si{n}^{2}A}$=$\frac{3}{5}$,
∴sinC=sin(A+B)=sinAcosB+cosAsinB=$\frac{4}{5}×\frac{\sqrt{2}}{2}+\frac{3}{5}×\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$.
(2)∵b=2$\sqrt{2}$,
∴由正弦定理可得:a=$\frac{bsinA}{sinB}$=$\frac{2\sqrt{2}×\frac{4}{5}}{\frac{\sqrt{2}}{2}}$=$\frac{16}{5}$,
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×\frac{16}{5}×2\sqrt{2}×\frac{7\sqrt{2}}{10}$=$\frac{112}{25}$.
点评 本题主要考查了同角三角函数关系式,两角和的正弦函数公式,正弦定理,三角形面积公式的应用,熟练掌握和灵活应用相关公式及定理是解题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知m,n是正实数,且n>m,若P=(1+m)n,Q=(1+n)m,则( )
| A. | P≥Q | B. | P<Q | ||
| C. | P>Q | D. | P,Q大小关系无法确定 |
20.点A(-2,m)关于点O(3,1)对称的点刚好落在直线x+y-1=0上,则m值为( )
| A. | -2 | B. | 3 | C. | 7 | D. | 9 |

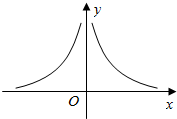 如图,幂函数y=x3m-7(m∈N)的图象关于y轴对称,且与x轴,y轴均无交点,求此函数的解析式及不等式f(x+2)<16的解集.
如图,幂函数y=x3m-7(m∈N)的图象关于y轴对称,且与x轴,y轴均无交点,求此函数的解析式及不等式f(x+2)<16的解集.