题目内容
14.分解因式4x4+1得(2x2+2x+1)(2x2-2x+1).分析 原式可化为4x4+4x2+1-4x2,再利用乘法公式即可得出.
解答 解:原式=4x4+4x2+1-4x2
=(2x2+1)2-(2x)2
=(2x2+2x+1)(2x2-2x+1).
故答案为:(2x2+2x+1)(2x2-2x+1).
点评 本题考查了乘法公式、因式分解方法,考查了计算能力,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
4.阅读下面的流程图,若输入a=5,b=-1,则输出的a值为( )
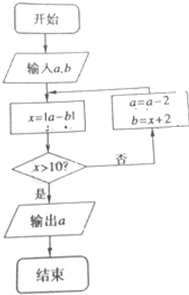

| A. | 16 | B. | 10 | C. | -3 | D. | -5 |
19.已知向量$\overrightarrow{OP}$=(1,1),$\overrightarrow{{OP}_{1}}$=(4,-4),且P2点分有向线段$\overrightarrow{P{P}_{1}}$所成的比为-2,则$\overrightarrow{{OP}_{2}}$的坐标是( )
| A. | (-$\frac{5}{2}$,$\frac{3}{2}$) | B. | ($\frac{5}{2}$,-$\frac{3}{2}$) | C. | (7,-9) | D. | (9,-7) |