题目内容
在△ABC中,内角A,B,C所对边长分别为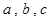 ,
,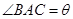 ,
,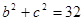 ,
, 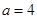 .
.
(1)求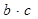 的最大值及
的最大值及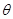 的取值范围;
的取值范围;
(2)求函数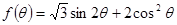 的最值. (本题满分12分)
的最值. (本题满分12分)
(1)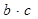 的最大值为16,0<
的最大值为16,0<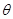
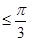
(2)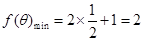 。
。 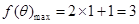 。
。
解析试题分析:①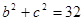
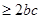 ,所以
,所以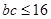 ;又由余弦定理
;又由余弦定理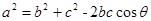 得:
得: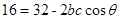 ,所以
,所以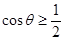 ,又
,又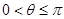 ,所以0<
,所以0<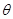
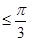
②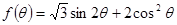
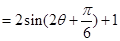 …………………………8分
…………………………8分
因为0<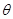
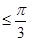 ,所以
,所以 <
<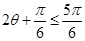 ,
, 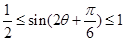 ,………………10分
,………………10分
当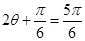 ,即
,即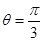 时,
时,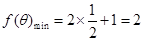 。 ……………………11分
。 ……………………11分
当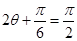 ,即
,即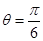 时,
时,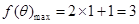 。 ……………………12分
。 ……………………12分
考点:本题考查基本不等式和三角函数的化一公式及利用三角函数的单调性求最值问题。
点评:三角函数和其他知识点相结合往往是第一道大题,一般较为简单,应该是必得分的题目。而有些同学在学习中认为这类题简单,自己一定会,从而忽略了对它的练习,因此导致考试时不能得满分,甚至不能得分。比如此题在第二问中,就较易忘掉应用第一问求出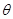 的范围。因此我们在平常训练的时候就要要求自己“会而对,对而全”。
的范围。因此我们在平常训练的时候就要要求自己“会而对,对而全”。

练习册系列答案
相关题目
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
(本小题满分14分)某公司生产的新产品的成本是2元/件,售价是3元/件,
年销售量为10万件,为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是 (万元)时,产品的销售量将是原销售量的
(万元)时,产品的销售量将是原销售量的 倍,且
倍,且 是
是 的二次函数,它们的关系如下表:
的二次函数,它们的关系如下表:
 | ··· | 1 | 2 | ··· | 5 | ··· |
 | ··· | 1.5 | 1.8 | ··· | 1.5 | ··· |
(2)求
 与
与 的函数关系式;
的函数关系式;(3)如果利润=销售总额
 成本费
成本费 广告费,试写出年利润S(万元)与广告费
广告费,试写出年利润S(万元)与广告费 (万元)的函数关系式;并求出当广告费
(万元)的函数关系式;并求出当广告费 为多少万元时,年利润S最大.
为多少万元时,年利润S最大. 
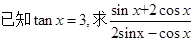
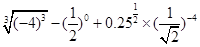 ;
;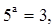
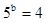 . 求a、b,并用
. 求a、b,并用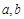 表示
表示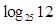 .
.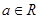 且
且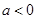 ,设函数
,设函数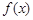 = ax2 +x-3alnx.
= ax2 +x-3alnx. 的单调区间;
的单调区间;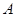 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品
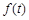 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;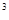 ,池底和池壁的造价分别为2
,池底和池壁的造价分别为2 元/
元/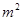 、
、 是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1
是二次函数,且f(0)=8及f(x+1)-f(x)=-2x+1 的单调递减区间及值域..
的单调递减区间及值域..