题目内容
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,都有
,都有![]() ;
;
(1)试证明数列![]() 是等差数列,并求其通项公式;
是等差数列,并求其通项公式;
(2)如果等比数列![]() 共有2017项,其首项与公比均为2,在数列
共有2017项,其首项与公比均为2,在数列![]() 的每相邻两项
的每相邻两项![]() 与
与![]() 之间插入
之间插入![]() 个
个![]()
![]() 后,得到一个新数列
后,得到一个新数列![]() ,求数列
,求数列![]() 中所有项的和;
中所有项的和;
(3)如果存在![]() ,使不等式
,使不等式![]() 成立,若存在,求实数
成立,若存在,求实数![]() 的范围,若不存在,请说明理由;
的范围,若不存在,请说明理由;
【答案】(1)见解析,![]() ;(2)
;(2)![]() ;(3)不存在;见解析
;(3)不存在;见解析
【解析】
(1)![]() 时,
时,![]() ;
;![]() 时,
时,![]() 即可证明。
即可证明。
(2)通过题意![]() ,写出前n项和式子,代入
,写出前n项和式子,代入![]() 即可求得数列
即可求得数列![]() 中所有项的和;(3)不等式
中所有项的和;(3)不等式![]() ,即不等式
,即不等式
![]() ,化为:
,化为:![]()
验证:![]() 时不等式不成立。
时不等式不成立。![]() 时,
时,![]() ,
,![]() ,即可求得结论。
,即可求得结论。
(1)证明:![]() 时,
时,![]() ;
;
![]() 时,
时,![]()
验证![]() 时也成立,所以数列
时也成立,所以数列![]() 是首项和公差都是1的等差数列。
是首项和公差都是1的等差数列。
(2)通过题意![]() , 则
, 则
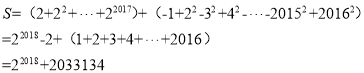
(3)不等式![]() ,
,
即不等式![]()
化为:![]()
因为![]() ,
,![]() ,而
,而![]() 时不等式不成立。
时不等式不成立。
![]() 时,
时,![]() ,
,![]() ,因此不存在
,因此不存在![]()
使得不等式![]() 成立。
成立。

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案【题目】2019年2月13日《西安市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.
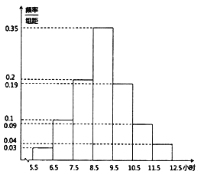
(1)求这200名学生每周阅读时间的样本平均数;
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?(精确到0.1)
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附: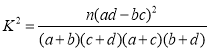 (
(![]() ).
).
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】“互联网+”是“智慧城市”的重要内容,A市在智慧城市的建设中,为方便市民使用互联网,在主城区覆盖了免费WiFi为了解免费WiFi在A市的使用情况,调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到如下列联表(单位:人):
经常使用免费WiFi | 尔或不用免费WiFi | 合计 | |
45岁及以下 | 70 | 30 | 100 |
45岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,判断是否有90%的把握认为A市使用免费WiFi的情况与年龄有关;
(2)现从所抽取的45岁以上的市民中按是否经常使用WiFi进行分层抽样再抽取5人.
(i)分别求这5人中经常使用,偶尔或不用免费WFi的人数;
(ii)从这5人中,再随机选出2人各赠送1件礼品,求选出的2人中至少有1人经常使用免费WiFi的概率.
附: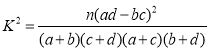 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |