题目内容
已知点M(-3,0),N(3,0),B(1,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2-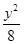 =1(x>1) =1(x>1) | B.x2-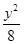 =1(x<-1) =1(x<-1) |
C.x2+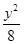 =1(x>0) =1(x>0) | D.x2-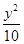 =1(x>1) =1(x>1) |
A
设另两个切点为E、F,如图所示,
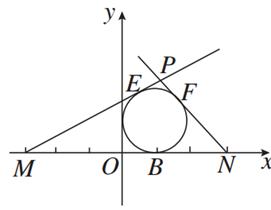
则|PE|=|PF|,|ME|=|MB|,|NF|=|NB|.
从而|PM|-|PN|=|ME|-|NF|
=|MB|-|NB|=4-2=2<|MN|,
∴P点的轨迹是以M、N为焦点,实轴长为2的双曲线的右支.
又∵a=1,c=3,∴b2=8.
故方程为x2-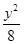 =1(x>1).
=1(x>1).

则|PE|=|PF|,|ME|=|MB|,|NF|=|NB|.
从而|PM|-|PN|=|ME|-|NF|
=|MB|-|NB|=4-2=2<|MN|,
∴P点的轨迹是以M、N为焦点,实轴长为2的双曲线的右支.
又∵a=1,c=3,∴b2=8.
故方程为x2-
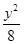 =1(x>1).
=1(x>1).
练习册系列答案
相关题目
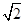 ,且过点(4,-
,且过点(4,-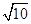 ).
).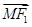 ·
· =0;
=0; =1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )
=1(a>0,b>0)的右焦点是抛物线y2=8x的焦点F,两曲线的一个公共点为P,且|PF| =5,则此双曲线的离心率为( )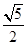

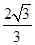
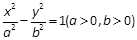 与抛物线
与抛物线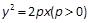 有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若
有一个共同的焦点F, 点M是双曲线与抛物线的一个交点, 若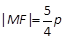 , 则此双曲线的离心率等于( ).
, 则此双曲线的离心率等于( ).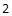

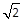

 -
-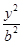 =1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )
=1(a>b>0)的左、右焦点分别为F1、F2,线段F1F2被抛物线y2=2bx的焦点分成7∶5的两段,则此双曲线的离心率为( )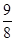
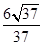

 x
x x
x x
x
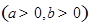 的一条渐近线平行于直线
的一条渐近线平行于直线 :
: ,双曲线的一个焦点在直线
,双曲线的一个焦点在直线
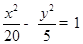
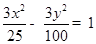
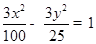
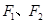 分别为双曲线
分别为双曲线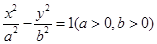 的左、右焦点,若在双曲线右支上存在点P,满足
的左、右焦点,若在双曲线右支上存在点P,满足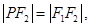 且
且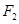 到直线
到直线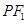 的距离等于双曲线的实轴长,则该双曲线的渐近线方程为
的距离等于双曲线的实轴长,则该双曲线的渐近线方程为