题目内容
已知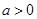 ,设命题
,设命题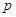 :函数
:函数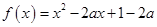 在区间
在区间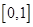 上与
上与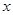 轴有两个不同的交点;命题
轴有两个不同的交点;命题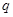 :
: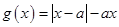 在区间
在区间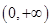 上有最小值.若
上有最小值.若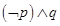 是真命题,求实数
是真命题,求实数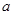 的取值范围.
的取值范围.
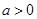 ,设命题
,设命题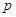 :函数
:函数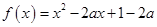 在区间
在区间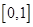 上与
上与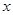 轴有两个不同的交点;命题
轴有两个不同的交点;命题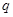 :
: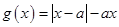 在区间
在区间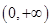 上有最小值.若
上有最小值.若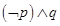 是真命题,求实数
是真命题,求实数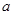 的取值范围.
的取值范围.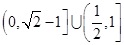
试题分析:先由
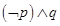 的真假性确定命题
的真假性确定命题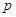 为假命题,
为假命题,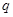 为真命题,然后就命题
为真命题,然后就命题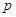 为真命题进行求解,结合二次函数的零点分布来讨论,最后在取答案时取参数范围的在
为真命题进行求解,结合二次函数的零点分布来讨论,最后在取答案时取参数范围的在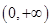 上的补集;对命题
上的补集;对命题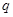 为真命题对
为真命题对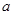 的范围进行求解,对于函数
的范围进行求解,对于函数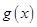 解析式化为分段函数,利用分段函数的单调性来考查.
解析式化为分段函数,利用分段函数的单调性来考查.试题解析:要使函数
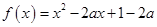 在
在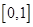 上与
上与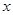 轴有两个不同的交点,
轴有两个不同的交点,必须
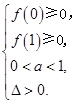 2分
2分即
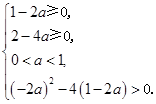 4分
4分解得
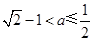 .
.所以当
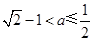 时,函数
时,函数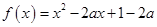 在
在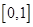 上与
上与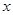 轴有两个不同的交点. 5分
轴有两个不同的交点. 5分下面求
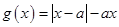 在
在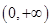 上有最小值时
上有最小值时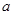 的取值范围:
的取值范围:方法1:因为
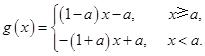 6分
6分①当
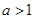 时,
时,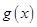 在
在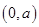 和
和 上单调递减,
上单调递减,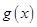 在
在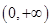 上无最小值; 7分
上无最小值; 7分②当
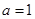 时,
时,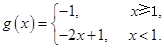
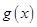 在
在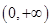 上有最小值
上有最小值 ; 8分
; 8分③当
 时,
时,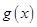 在
在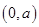 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,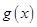 在
在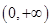 上有最小值
上有最小值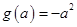 . 9分
. 9分所以当
 时,函数
时,函数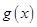 在
在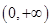 上有最小值. 10分
上有最小值. 10分方法2:因为
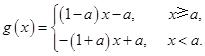 6分
6分因为
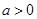 ,所以
,所以 .
.所以函数
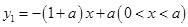 是单调递减的. 7分
是单调递减的. 7分要使
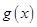 在
在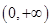 上有最小值,必须使
上有最小值,必须使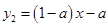 在
在 上单调递增或为常数. 8分
上单调递增或为常数. 8分即
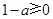 ,即
,即 . 9分
. 9分所以当
 时,函数
时,函数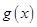 在
在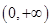 上有最小值. 10分
上有最小值. 10分若
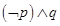 是真命题,则
是真命题,则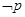 是真命题且
是真命题且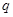 是真命题,即
是真命题,即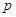 是假命题且
是假命题且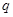 是真命题. 11分
是真命题. 11分所以
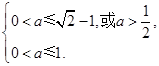 12分
12分解得
 或
或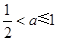 . 13分
. 13分故实数
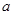 的取值范围为
的取值范围为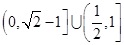 . 14分
. 14分
练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
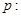 关于
关于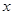 的不等式
的不等式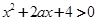 对一切
对一切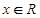 恒成立;命题
恒成立;命题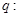 函数
函数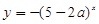 是减函数,若
是减函数,若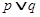 为真命题,
为真命题,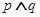 为假命题,则实数
为假命题,则实数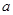 的取值范围为 .
的取值范围为 .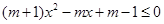 ”是假命题,则实数m的取值范围是__________.
”是假命题,则实数m的取值范围是__________.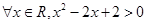 ”的否定是 .
”的否定是 . ,并设:
,并设:
 ,
, 至少有3个实根;
至少有3个实根; 当
当 时,方程
时,方程 当
当 时,方程
时,方程



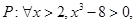 那么
那么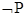 是
是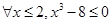
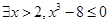
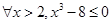
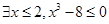
 :函数
:函数 在R为增函数,
在R为增函数, :函数
:函数 在R为减函数,
在R为减函数, :
: ,
, :
: ,
, :
: 和
和 :
: 中,真命题是( )
中,真命题是( )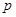 :
: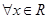 ,
,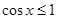 ,则
,则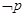 :
: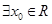 ,
,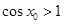
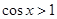
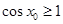
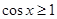
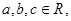 则“
则“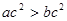 ”是“
”是“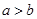 ”成立的充分不必要条件;
”成立的充分不必要条件;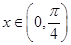 时,函数
时,函数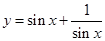 的最小值为2;
的最小值为2;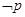 ”与命题“
”与命题“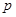 或
或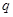 ”都是真命题,则命题
”都是真命题,则命题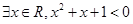 ,则
,则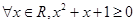 .
.