题目内容
8.函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-ax+5,x≤1}\\{1+\frac{1}{x},x>1}\end{array}\right.$在定义域R上不是单调函数,则a的取值范围是a>4或a<2.分析 先判断函数为单调函数时的条件,即可得到结论.
解答 解:若f(x)在R上为单调函数,
∵当x>1时,函数f(x)为减函数,
∴函数在(-∞,+∞)上为减函数,
则满足$\left\{\begin{array}{l}{-\frac{-a}{2}=\frac{a}{2}≥1}\\{1-a+5≥1+1}\end{array}\right.$,即$\left\{\begin{array}{l}{a≥2}\\{a≤4}\end{array}\right.$,
解得2≤a≤4,
若函数f(x)在R上不是单调函数,
则a>4或a<2,
故答案为:a>4或a<2.
点评 本题主要考查复合函数的单调性的应用,利用条件先求出函数为单调函数的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知曲线f(x)=e2x-2ex+ax-1存在两条斜率为3的切线,则实数a的取值范围为( )
| A. | (3,+∞) | B. | (3,$\frac{7}{2}$) | C. | (-∞,$\frac{7}{2}$) | D. | (0,3) |
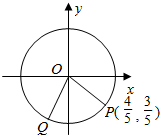 已知角α、β的终边分别与⊙O:x2+y2=1交于点P($\frac{4}{5}$,-$\frac{3}{5}$)、且OP⊥OQ,则sinα=-$\frac{3}{5}$,tanβ=$\frac{4}{3}$.
已知角α、β的终边分别与⊙O:x2+y2=1交于点P($\frac{4}{5}$,-$\frac{3}{5}$)、且OP⊥OQ,则sinα=-$\frac{3}{5}$,tanβ=$\frac{4}{3}$.