题目内容
【题目】已知数列{an}、{bn}都是公差为1的等差数列,其首项分别为a1、b1 , 且a1+b1=5,a1 , b1∈N* , 设cn=a ![]() ,则数列{cn}的前10项和等于( )
,则数列{cn}的前10项和等于( )
A.55
B.70
C.85
D.100
【答案】C
【解析】解:∵a1+b1=5,a1 , b1∈N* , ∴a1 , b1有1和4,2和3,3和2,4和1四种可能,
当a1 , b1为1和4的时,c1= ![]() =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
当a1 , b1为2和3的时,c1= ![]() =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
当a1 , b1为4和1的时,c1= ![]() =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
当a1 , b1为3和2的时,c1= ![]() =4,前10项和为4+5+…+12+13=85;
=4,前10项和为4+5+…+12+13=85;
故数列{cn}的前10项和等于85,
故选:C.
a1 , b1有1和4,2和3,3和2,4和1四种可能,由此进行分类讨论,利用等差数列的性质能求出数列{cn}的前10项和.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
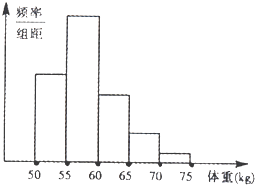
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:![]() ),其频率分布直方图如下:
),其频率分布直方图如下:

(1)估计旧养殖法的箱产量低于50![]() 的概率并估计新养殖法的箱产量的平均值;
的概率并估计新养殖法的箱产量的平均值;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | 合计 | |
旧养殖法 | |||
新养殖法 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参考数据:![]()