题目内容
在平面直角坐标系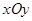 中,抛物线C的顶点在原点,焦点F的坐标为(1,0)。
中,抛物线C的顶点在原点,焦点F的坐标为(1,0)。
(1)求抛物线C的标准方程;
(2)设M、N是抛物线C的准线上的两个动点,且它们的纵坐标之积为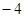 ,直线MO、NO与抛物线的交点分别为点A、B,求证:动直线AB恒过一个定点。
,直线MO、NO与抛物线的交点分别为点A、B,求证:动直线AB恒过一个定点。
(1)设抛物线的标准方程为 ,则
,则 ,
,
所以抛物线方程为
(2)直线MO的方程: ,与
,与 联立解得A点坐标
联立解得A点坐标 ,B点坐标
,B点坐标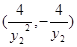 ,得出直线AB的方程为:
,得出直线AB的方程为: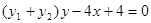 ,说明直线AB恒过定点(1,0)。
,说明直线AB恒过定点(1,0)。
解析试题分析:(1)设抛物线的标准方程为 ,则
,则 ,
,
所以抛物线方程为
(2)抛物线C的准线方程为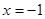 ,设
,设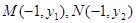 ,其中
,其中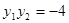 ,
,
直线MO的方程: ,将
,将 与
与 联立解得A点坐标
联立解得A点坐标 。
。
同理可得B点坐标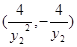 ,则直线AB的方程为:
,则直线AB的方程为:
整理得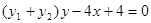 ,故直线AB恒过定点(1,0)。
,故直线AB恒过定点(1,0)。
考点:本题主要考查直线方程,抛物线标准方程,直线与抛物线的位置关系。
点评:中档题,曲线关系问题,往往通过联立方程组,得到一元二次方程,运用韦达定理。本题求抛物线标准方程时,主要运用了抛物线的几何性质。(2)证明直线过定点问题时,巧妙地假设,并应用假设字母表示点的坐标,值得学习。

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
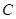 的圆心为原点
的圆心为原点 ,且与直线
,且与直线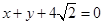 相切。
相切。
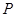 在直线
在直线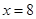 上,过
上,过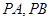 ,切点为
,切点为 ,求证:直线
,求证:直线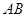 恒过定点。
恒过定点。 ,椭圆
,椭圆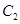 以
以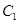 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线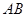 的方程.
的方程.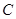 的顶点为坐标原点
的顶点为坐标原点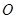 ,焦点
,焦点 在
在 轴上,准线
轴上,准线 与圆
与圆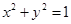 相切.
相切.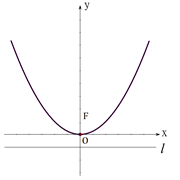
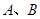 在抛物线
在抛物线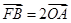 ,求点
,求点 的坐标.
的坐标. 的离心率为
的离心率为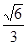 ,
, 为椭圆的右焦点,
为椭圆的右焦点,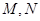 两点在椭圆
两点在椭圆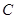 上,且
上,且 ,定点
,定点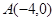 。
。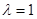 时,有
时,有 ,求椭圆
,求椭圆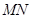 斜率为k,且设
斜率为k,且设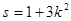 时,试求
时,试求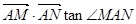 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。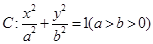 的焦点为
的焦点为 、
、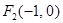 ,离心率为
,离心率为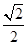 ,过点
,过点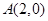 的直线
的直线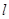 交椭圆
交椭圆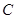 于
于 、
、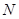 两点.
两点.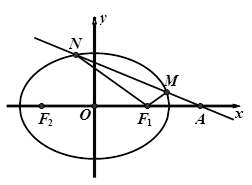
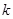 的取值范围;
的取值范围;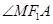 和
和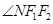 是否总相等?若相等,请给出证明,若不相等,说明理由.
是否总相等?若相等,请给出证明,若不相等,说明理由.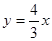 ,右焦点
,右焦点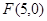 ,双曲线的实轴为
,双曲线的实轴为 ,
,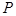 为双曲线上一点(不同于
为双曲线上一点(不同于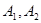 ),直线
),直线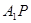 ,
,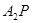 分别与直线
分别与直线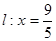 交于
交于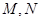 两点
两点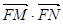 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。