题目内容
(本小题满分14分)
已知数列 的前n项和
的前n项和 满足:
满足: (
( 为常数,
为常数, )
)
(Ⅰ)求 的通项公
的通项公 式;
式;
(Ⅱ)设 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;
的值;
(Ⅲ)在满足条件(Ⅱ)的情形下, ,数列
,数列 的前n项和为
的前n项和为 .
.
求证: .
.
已知数列
 的前n项和
的前n项和 满足:
满足: (
( 为常数,
为常数, )
)(Ⅰ)求
 的通项公
的通项公 式;
式;(Ⅱ)设
 ,若数列
,若数列 为等比数列,求
为等比数列,求 的值;
的值;(Ⅲ)在满足条件(Ⅱ)的情形下,
 ,数列
,数列 的前n项和为
的前n项和为 .
. 求证:
 .
.解:(Ⅰ)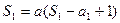
∴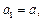 ……….1分
……….1分
当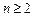 时,
时, 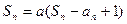
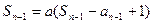
两式相减得: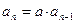 ,
,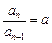 (a≠0,n≥2),即
(a≠0,n≥2),即 是等比数列.
是等比数列.
∴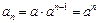 ;…5分
;…5分
(Ⅱ)由(Ⅰ)知a≠1
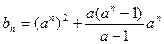 ,
,
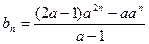 ,
,
若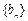 为等比数列,则有
为等比数列,则有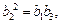
而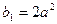 ,
,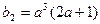
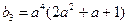 ……7分
……7分
故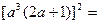
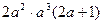 ,
,
解得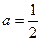 , ……………………9分
, ……………………9分
再将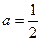 代入得
代入得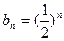 成立,
成立,
所以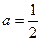 . …………10分
. …………10分
(III)证明:由(Ⅱ)知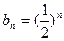 ,
,
所以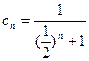
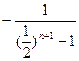 ,
,
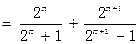
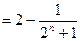
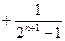 … 12分
… 12分
所以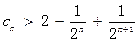
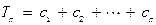
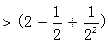
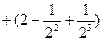

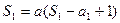
∴
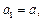 ……….1分
……….1分当
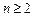 时,
时, 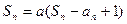
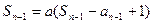
两式相减得:
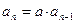 ,
,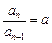 (a≠0,n≥2),即
(a≠0,n≥2),即 是等比数列.
是等比数列.∴
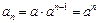 ;…5分
;…5分(Ⅱ)由(Ⅰ)知a≠1
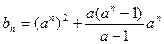 ,
,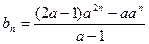 ,
,若
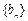 为等比数列,则有
为等比数列,则有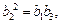
而
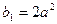 ,
,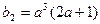
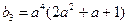 ……7分
……7分故
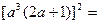
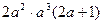 ,
,解得
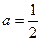 , ……………………9分
, ……………………9分再将
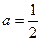 代入得
代入得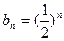 成立,
成立,所以
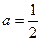 . …………10分
. …………10分(III)证明:由(Ⅱ)知
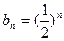 ,
,所以
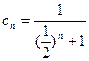
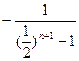 ,
,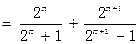
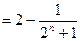
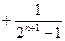 … 12分
… 12分所以
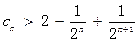
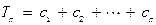
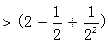
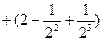

略

练习册系列答案
相关题目
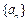 是以a为首项,q为公比的等比数列,
是以a为首项,q为公比的等比数列,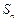 为它的前n项和.
为它的前n项和.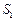 、
、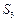 、
、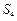 成等差数列时,求q的值;
成等差数列时,求q的值;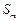 、
、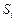 成等差数列时,求证:对任意自然数k,
成等差数列时,求证:对任意自然数k,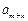 、
、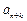 、
、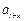 也成等差数列.
也成等差数列.
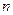 个等式为
个等式为 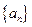 满足
满足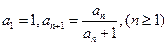 ,数列
,数列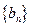 满足
满足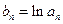 ,数列
,数列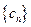
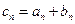 .
.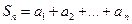 ,
,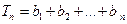 ,试比较
,试比较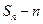 与
与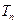 的大小,并证明;
的大小,并证明;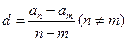 是一个常数,显然在本题的数列
是一个常数,显然在本题的数列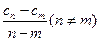 不是一个常数,但
不是一个常数,但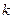 呢,若会,请求出
呢,若会,请求出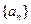 的前
的前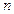 项和
项和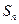 满足
满足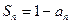
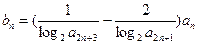 ,求证:
,求证: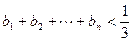
 满足
满足 ,则
,则 =( )
=( )


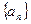 是等差数列,前n项和为Sn,
是等差数列,前n项和为Sn,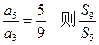 =
= 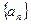 中,
中,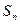 =40,
=40,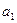 =13,d="-2" 时,n=__________.
=13,d="-2" 时,n=__________. 。
。