题目内容
9.已知数列{an}的通项an=$\frac{nx}{(x+1)(2x+1)…(nx+1)}$,n∈N*,若a1+a2+a3<1,则实数x可能等于( )| A. | -$\frac{3}{2}$ | B. | -$\frac{5}{12}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{11}{24}$ |
分析 由数列的递推公式可得a1+a2+a3=$\frac{x}{x+1}$+$\frac{2x}{(x+1)(2x+1)}$+$\frac{3x}{(x+1)(2x+1)(3x+1)}$,解关于x的不等式结合选项可得.
解答 解:∵数列{an}的通项an=$\frac{nx}{(x+1)(2x+1)…(nx+1)}$,
∴a1+a2+a3=$\frac{x}{x+1}$+$\frac{2x}{(x+1)(2x+1)}$+$\frac{3x}{(x+1)(2x+1)(3x+1)}$
=$\frac{x(2x+1)(3x+1)+2x(3x+1)+3x}{(x+1)(2x+1)(3x+1)}$=$\frac{x(6{x}^{2}+11x+6)}{(x+1)(2x+1)(3x+1)}$,
∵a1+a2+a3<1,∴$\frac{x(6{x}^{2}+11x+6)}{(x+1)(2x+1)(3x+1)}$<1,
∴$\frac{x(6{x}^{2}+11x+6)}{(x+1)(2x+1)(3x+1)}$-1<0,
通分整理可得$\frac{-1}{(x+1)(2x+1)(3x+1)}$<0,
∴(x+1)(2x+1)(3x+1)>0,
解得x>-$\frac{1}{3}$或-1<x<-$\frac{1}{2}$,
故选:C
点评 本题考查数列的递推公式,涉及分式不等式的解集,属中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
4.若x,y是非负整数,那么满足方程25+y2=x2的解有( )
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
14.已知向量$\overrightarrow{a}$=(sinθ,-2)与$\overrightarrow{b}$=(1,cosθ)互相垂直,其中θ∈$(0,\frac{π}{2})$,则sinθ+cosθ等于( )
| A. | $\frac{{-\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
 如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.
如图,四边形ABCD中,AB∥DC,AB,BC,DC,AD(或其延长线)分别与平面M相交于E,F,G,H,求证:E,F,G,H必在同一直线上.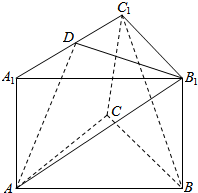 如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.
如图,三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长为$\frac{\sqrt{2}}{2}$a,点D在棱A1C1上.