题目内容
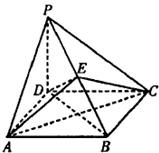 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,PD=8,AC=6,BD=8,AC∩BD=O,E是棱PB上的一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD为菱形,PD=8,AC=6,BD=8,AC∩BD=O,E是棱PB上的一点.(1)求证:AC⊥DE;
(2)若BE:EP=1:2,求三棱锥O-BCE的体积;
(3)是否存在点E,使△ACE的面积最小?若存在,试求出△ACE面积最小值及对应线段BE的长;若不存在,请说明理由.
分析:(1)菱形的对角线AC、BD互相垂直,用线面垂直的定义得到AC、PD互相垂直,结合线面垂直的判定定理,得到AC与平面PBD垂直,最终得到AC与DE互相垂直.
(2)根据点E是线段PB靠近B点的一个三等分点,得到E到平面ABCD的距离等于PD长的
,再用菱形的性质得到S△OBC=
S菱形ABCD=6,最后用棱锥的体积公式得出三棱锥O-BCE的体积.
(3)连接OE,可以根据AC与平面PBD垂直,得到OE就是三角形AEC的边AC上的高,OE最短时△ACE的面积也达到最小值,转化为点O到线段PB的最小距离问题.由此得到当OE⊥PB时,△ACE的面积最小,再利用等腰直角三角形OEB求出此时的OE长,问题得到解决.
(2)根据点E是线段PB靠近B点的一个三等分点,得到E到平面ABCD的距离等于PD长的
| 1 |
| 3 |
| 1 |
| 4 |
(3)连接OE,可以根据AC与平面PBD垂直,得到OE就是三角形AEC的边AC上的高,OE最短时△ACE的面积也达到最小值,转化为点O到线段PB的最小距离问题.由此得到当OE⊥PB时,△ACE的面积最小,再利用等腰直角三角形OEB求出此时的OE长,问题得到解决.
解答:解:(1)
⇒AC⊥PD
∵四边形ABCD为菱形
∴AC⊥BD结合PD与DB相交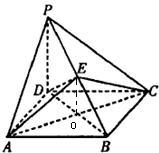
∴AC⊥平面PDB
∵DE?平面PDB
∴AC⊥DE…4′
(2)即求三棱锥E-OBC的体积,
由BE:EP=1:2及PD=8,
得:E到平面ABCD的距离为
又四边形ABCD为菱形,AC=6,BD=8,
∴S△OBC=
S菱形ABCD=
×
×6×8=6
∴VO-BCE=
…10′
(3)连接OE,由(1)得AC⊥平面PDB,而OE?平面PDB
∴OE⊥AC,OE是三角形ACE的边AC上的高
∴S△ACE=
AC•OE=3OE,当OE最短时,△ACE的面积最小,
因为点E在线段PB上运动,所以当OE⊥PB时,△ACE的面积最小,
此时Rt△OEB是以OB为斜边的等腰直角三角形,
∴OE=
OB=
BD=2
,
所以存在点E使△ACE的面积最小,且△ACE面积最小值为6
,此时BE的长为2
…14′
|
∵四边形ABCD为菱形
∴AC⊥BD结合PD与DB相交

∴AC⊥平面PDB
∵DE?平面PDB
∴AC⊥DE…4′
(2)即求三棱锥E-OBC的体积,
由BE:EP=1:2及PD=8,
得:E到平面ABCD的距离为
| 8 |
| 3 |
又四边形ABCD为菱形,AC=6,BD=8,
∴S△OBC=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴VO-BCE=
| 16 |
| 3 |
(3)连接OE,由(1)得AC⊥平面PDB,而OE?平面PDB
∴OE⊥AC,OE是三角形ACE的边AC上的高
∴S△ACE=
| 1 |
| 2 |
因为点E在线段PB上运动,所以当OE⊥PB时,△ACE的面积最小,
此时Rt△OEB是以OB为斜边的等腰直角三角形,
∴OE=
| ||
| 2 |
| ||
| 4 |
| 2 |
所以存在点E使△ACE的面积最小,且△ACE面积最小值为6
| 2 |
| 2 |
点评:本题综合了直线与平面平行的判定、直线与平面垂直的性质和棱柱、棱锥、棱台的体积等几个知识点,属于中档题.在题中出现了探究性问题,请同学们留意在解题过程中“空间问题平面化的思路”,是立体几何常用的数学思想.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.