题目内容
5.已知f(x-1)=x2+6x,则f(x)的表达式是( )| A. | x2+4x-5 | B. | x2+8x+7 | C. | x2+2x-3 | D. | x2+6x-10 |
分析 f(x-1)=x2+6x,设x-1=t,则x=t+1,于是f(t)=(t+1)2+6(t+1),化简并且把t与x互换即可得出.
解答 解:∵f(x-1)=x2+6x,
设x-1=t,则x=t+1,
∴f(t)=(t+1)2+6(t+1)=t2+8t+7,
把t与x互换可得:f(x)=x2+8x+7.
故选:B.
点评 本题考查了指数函数的图象与性质,考查了数形结合方法、推理能力与计算能力,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
16.算法如果执行下面的程序框图,输入n=6,m=4,那么输出的p于( )
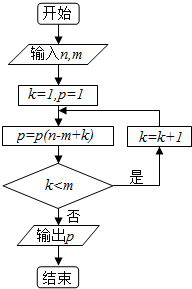

| A. | 12 | B. | 60 | C. | 360 | D. | 48 |
17.将函数f(2x)的图象向左平移1个单位长度,所得图象与g(x)=lnx的图象关于直线y=x对称,则f(x)等于( )
| A. | ex-1 | B. | ${e^{1-\frac{x}{2}}}$ | C. | ${e^{\frac{x}{2}-1}}$ | D. | e1-x |
13.已知条件p:log2(x-1)<1;条件q:|x-1|<1,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分不又不必要条件 |
20.若全集U=R,A=[1,3],B={x|x2-2x≤0},则A∩(∁UB)=( )
| A. | [1,2] | B. | (-∞,0)∪(2,3] | C. | [0,1) | D. | (2,3] |
10.已知集合S={(x,y)|x+y=4},T={(x,y)|x-y=2},那么集合S∩T=( )
| A. | {3,1} | B. | (3,1) | C. | x=3,y=1 | D. | {(3,1)} |
13.化简$\sqrt{(a-b)^{2}}+\root{5}{(a-b)^{5}}$的结果是( )
| A. | 0 | B. | 2(b-a) | C. | 0或2(a-b) | D. | b-a |