题目内容
【题目】双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 为坐标原点.
为坐标原点.![]() 为曲线
为曲线![]() 右支上的点,点
右支上的点,点![]() 在
在![]() 外角平分线上,且
外角平分线上,且![]() .若
.若![]() 恰为顶角为
恰为顶角为![]() 的等腰三角形,则该双曲线的离心率为( )
的等腰三角形,则该双曲线的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,根据几何关系,求得
,根据几何关系,求得![]() 点坐标,代入双曲线方程可得
点坐标,代入双曲线方程可得![]() 齐次式,则问题得解.
齐次式,则问题得解.
延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() ,如下所示:
,如下所示:

不妨设![]() ,
,
因为![]() ,且
,且![]() 为
为![]() 的角平分线,故可得
的角平分线,故可得![]() ,
,
故可得![]() ,且
,且![]() 为
为![]() 的中点;
的中点;
因为![]() 为顶角
为顶角![]() 的等腰三角形,故可得
的等腰三角形,故可得![]() ,
,
由余弦定理可得![]() ,
,
在![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,故
的中点,故![]() ;
;
根据双曲线定义可知:![]() ,即
,即![]() ;
;
又![]() ;
;
联立可得![]() ;
;
因为![]() 为顶角
为顶角![]() 的等腰三角形
的等腰三角形
故在直角三角形![]() 中,
中,![]()
则![]() ,由勾股定理可得
,由勾股定理可得![]()
故可得![]() 点坐标为
点坐标为 ,即
,即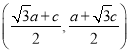 ,代入双曲线方程可得:
,代入双曲线方程可得:
 ,
,
整理得:![]() ,
,
同除![]() 可得
可得![]() ,
,
分解因式可得![]() ,
,
解得![]() 或
或![]() (舍去负根),
(舍去负根),
则![]() .
.
故选:D.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目