题目内容
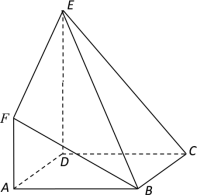
【题目】如图,在多面体![]() 中,梯形
中,梯形![]() 与平行四边形
与平行四边形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)根据线线平行得线面平行![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再根据线面平行得面面平行平面
,再根据线面平行得面面平行平面![]() 平面
平面![]() ,最后由面面平行性质得结论,(Ⅱ)先根据面面垂直得线面垂直
,最后由面面平行性质得结论,(Ⅱ)先根据面面垂直得线面垂直![]() 平面
平面![]() ,再得线线垂直
,再得线线垂直![]() ,类似可得
,类似可得![]() 进而建立空间直角坐标系,设立各点坐标,利用方程组解得平面
进而建立空间直角坐标系,设立各点坐标,利用方程组解得平面![]() 法向量,利用向量数量积得两法向量夹角,最后根据二面角与法向量夹角关系得结果,(Ⅲ)先设
法向量,利用向量数量积得两法向量夹角,最后根据二面角与法向量夹角关系得结果,(Ⅲ)先设![]() ,再利用方程组解得平面
,再利用方程组解得平面![]() 法向量,最后根据两法向量数量积为零解得结果.
法向量,最后根据两法向量数量积为零解得结果.
(Ⅰ)由底面![]() 为平行四边形,知
为平行四边形,知![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() , 所以
, 所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() ,又因为
,又因为![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(Ⅱ)连接![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() . 则
. 则![]() .
.
又因为![]() ,
,![]() ,
,![]() , 所以
, 所以![]() 平面
平面![]() ,则
,则![]() .
.
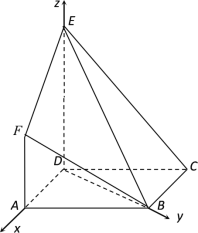
故![]() 两两垂直,所以以
两两垂直,所以以![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴和
轴和![]() 轴,如图建立空间直角坐标系,则
轴,如图建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() , 所以
, 所以![]() ,
,![]() ,
,![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由![]() ,
,![]() ,得
,得![]() 令
令![]() ,得
,得![]() .
.
所以![]() .
.
如图可得二面角![]() 为锐角, 所以二面角
为锐角, 所以二面角![]() 的余弦值为
的余弦值为![]() .
.
(Ⅲ)结论:线段![]() 上存在点
上存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
证明如下:设![]() ,所以
,所以![]() . 设平面
. 设平面![]() 的法向量为
的法向量为![]() ,又因为
,又因为![]() ,所以
,所以![]() ,
,![]() ,即
,即![]() 令
令![]() ,得
,得![]() .
.
若平面![]() 平面
平面![]() ,则
,则![]() ,即
,即![]() , 解得
, 解得![]() .
.
所以线段![]() 上存在点
上存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,且此时
,且此时![]() .
.

【题目】团体购买公园门票,票价如下表:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
现某单位要组织其市场部和生产部的员工游览该公园,这两个部门人数分别为a和b![]() ,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数
,若按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;若两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元,那么这两个部门的人数![]() ____;
____;![]() ____.
____.