题目内容
设f(x)＝x3＋log2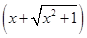
，则不等式f(m)＋f(m2－2)≥0(m∈R)成立的充要条件是________．(注：填写m的取值范围)
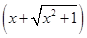，则不等式f(m)＋f(m2－2)≥0(m∈R)成立的充要条件是________．(注：填写m的取值范围)m≥1或m≤－2
判断函数是奇函数，且在R上是递增函数，∴f(m)＋f(m2－2)≥0即为f(m2－2)≥－f(m)＝f(－m)，∴m2－2≥－m，解得m≥1或m≤－2.
练习册系列答案
相关题目
题目内容
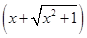，则不等式f(m)＋f(m2－2)≥0(m∈R)成立的充要条件是________．(注：填写m的取值范围)
，其中
是常数．
是奇函数，求
轴．
]恒成立,则a的最小值是( )
的单调区间表述正确的是( )
中，满足“对任意的
时，均有
”的是（ ）
