题目内容
位于函数 的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以
的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以 为首项,-1为公差的等差数列xn.
为首项,-1为公差的等差数列xn.(1)求点Pn的坐标;
(2)设抛物线C1,C2,C3,…Cn,…中的第一条的对称轴都垂直于x轴,对于n∈N*第n条抛物线Cn的顶点为Pn,抛物线Cn过点Dn(0,n2+1),且在该点处的切线的斜率为kn,求证
 .
.
【答案】分析:(1)位于函数 的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以
的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以 为首项,-1为公差的等差数列xn
为首项,-1为公差的等差数列xn
(2)欲证 ,关键是求得
,关键是求得 .先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得
.先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得  .
.
解答:解:(1)由于Pn的横坐标构成以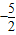 为首项,-1为公差的等差数列{xn},
为首项,-1为公差的等差数列{xn},
故 .
.
又Pn(xn,yn)位于函数 的图象上,
的图象上,
所以y .
.
所求点Pn(xn,yn)的坐标为( .
.
(2)∵Cn的对称轴垂直于x轴,且顶点为Pn,
∴设Cn的方程为 .
.
把Dn(0,n2+1)代入上式,得a=1,
∴Cn的方程为y=x2+(2n+3)x+n2+1.
∵kn=y'|x=0=2n+3,
∴ ,
,
∴ =
=
= .
.
故得: .
.
点评:本题考查的知识点是等差数列的通项公式,及直线的方程,由由Pn的横坐标构成等差数列{xn},我们不难根据已知求出数列{xn}的通项公式,代入直线方程,求出对应的纵坐标,即可得到点的坐标.本题还考查了数列求和问题.考查了用裂项法求和的方法运用和对数列基础知识的综合运用.
 的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以
的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…这一系列点的横坐标构成以 为首项,-1为公差的等差数列xn
为首项,-1为公差的等差数列xn(2)欲证
 ,关键是求得
,关键是求得 .先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得
.先设出Cn的方程,把D点代入求得a,进而对函数进行求得求得切线的斜率,即kn的表达式,进而用裂项法求得  .
.解答:解:(1)由于Pn的横坐标构成以
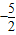 为首项,-1为公差的等差数列{xn},
为首项,-1为公差的等差数列{xn},故
 .
.又Pn(xn,yn)位于函数
 的图象上,
的图象上,所以y
 .
.所求点Pn(xn,yn)的坐标为(
 .
.(2)∵Cn的对称轴垂直于x轴,且顶点为Pn,
∴设Cn的方程为
 .
.把Dn(0,n2+1)代入上式,得a=1,
∴Cn的方程为y=x2+(2n+3)x+n2+1.
∵kn=y'|x=0=2n+3,
∴
 ,
,∴
 =
=
=
 .
.故得:
 .
.点评:本题考查的知识点是等差数列的通项公式,及直线的方程,由由Pn的横坐标构成等差数列{xn},我们不难根据已知求出数列{xn}的通项公式,代入直线方程,求出对应的纵坐标,即可得到点的坐标.本题还考查了数列求和问题.考查了用裂项法求和的方法运用和对数列基础知识的综合运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,这一系列点的横坐标构成以-
的图象上的一系列点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…,这一系列点的横坐标构成以- 为首项,-1为公差的等差数列{xn}。
为首项,-1为公差的等差数列{xn}。 。
。