题目内容
在直角坐标平面上有一点列P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…对每个正整数n,点Pn位于函数![]() 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(1)求点Pn的坐标;
(2)设抛物线列C1,C2,C3,…,Cn,…中的每一条的对称轴都垂直于x轴,第n条抛物线Cn的顶点为Pn且过点Dn(0,n2+1),记过点Dn且与抛物线Cn只有一个交点的直线的斜率为kn,求证:![]() .
.
(3)设![]() ,
,![]() ,等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,-265<a10<-125,求{an}的通项公式.
,等差数列{an}的任一项an∈S∩T,其中a1是S∩T中的最大数,-265<a10<-125,求{an}的通项公式.
答案:
解析:
解析:
|
答案:(1)∵Pn的横坐标构成以 ∴ ∵ ∴ ∴点Pn的坐标为 (2)据题意可设抛物线Cn的方程为: 即 ∵抛物线Cn过点Dn(0,n2+1) ∴ ∴ ∵过点Dn且与抛物线Cn只有一个交点的直线即为以Dn为切点的切线 ∴ ∴ ∴ ∴ (3)∵ ∴S∩T中的元素即为两个等差数列{-2n-3}与{-12n-5}中的公共项,它们组成以-17为首项,以-12为公差的等差数列 ∵ ∴a1=-17,其公差为 1°当k=1时, 此时 2°当k=2时, 此时 3°当k=3时, 此时 4°k>3时,不满足题意. 综上所述所求通项为 |

练习册系列答案
相关题目
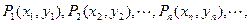 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数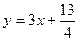 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以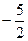 为首项,-1为公差的等
为首项,-1为公差的等 差数列{xn}.
差数列{xn}.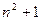 ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求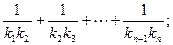
 设
设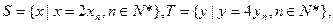 等差数列
等差数列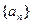 的任一项
的任一项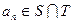 ,其中
,其中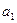 是
是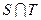 中的最大数,
中的最大数,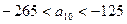 ,求数列
,求数列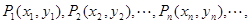 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数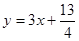 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以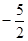 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}. ).记与抛物线Cn相切于点Dn的直线的斜率为kn,求
).记与抛物线Cn相切于点Dn的直线的斜率为kn,求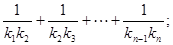
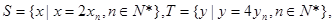 等差数列
等差数列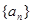 的任一项
的任一项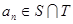 ,其中
,其中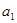 是
是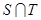 中的最大数,
中的最大数,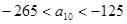 ,求数列
,求数列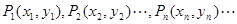 ,对一切正整数
,对一切正整数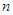 ,点
,点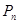 位于函数
位于函数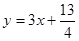 的图象上,且
的图象上,且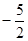 为首项,
为首项,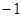 为公差的等差数列
为公差的等差数列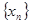 。
。 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于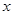 轴,第
轴,第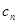 的顶点为
的顶点为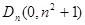 ,记与数列
,记与数列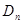 的直线的斜率为
的直线的斜率为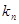 ,求:
,求: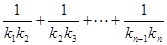 。
。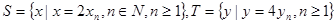 ,等差数列
,等差数列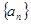 的任一项
的任一项 ,其中
,其中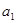 是
是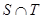 中的最大数,
中的最大数,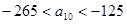 ,求
,求