题目内容
(本小题满分14分)
已知点 、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 轴于点
轴于点 和点
和点 ,
,
(Ⅰ)用 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;
(Ⅱ)某同学发现,当曲线C的方程为: 时,
时, 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,
 的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
【答案】
解:(Ⅰ)依题意N(k,-l),且∵klmn≠0及MP、NP与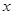 轴有交点知:……2分
轴有交点知:……2分
M、P、N为不同点,直线PM的方程为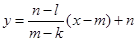 ,……3分
,……3分
则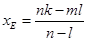 ,同理可得
,同理可得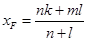 …6分
…6分
(Ⅱ)∵M,P在椭圆C: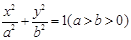 上,
上,
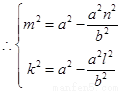 ,
,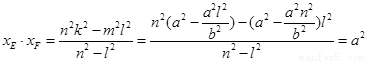 (定值).
(定值).
∴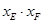 的值是与点M、N、P位置无关
. ……………11分
的值是与点M、N、P位置无关
. ……………11分
(Ⅲ)一个探究结论是: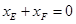 .
………………………14分
.
………………………14分
提示:依题意, 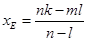 ,
,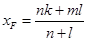 .
.
∵M,P在抛物线C:y2=2px(p>0)上,
∴n2=2pm,l2=2pk.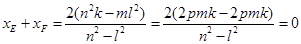 .
.
∴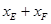 为定值.
为定值.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)