题目内容
已知函数f(x)=cos(2x-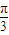 )+sin2x-cos2x.
)+sin2x-cos2x.(I)求函数f(x)的单调减区间;
(II)若f(a)=
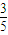 ,2a是第一象限角,求sin2a的值.
,2a是第一象限角,求sin2a的值.
【答案】分析:(I)利用两角差的余弦公式,二倍角公式化简函数f(x)=sin(2x-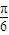 ),由2kπ+
),由2kπ+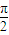 ≤x≤2kπ+
≤x≤2kπ+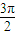 ,k∈z,求出
,k∈z,求出
函数f(x)的减区间.
(II)根据sin(2a- )=
)=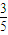 ,2kπ-
,2kπ-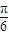 <2a-
<2a-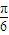 <2kπ+
<2kπ+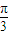 ,k∈z,利用同角三角函数的基本关系 求出cos(2a-
,k∈z,利用同角三角函数的基本关系 求出cos(2a-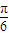 )
)
的值,由sin2a=sin[(2a-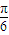 )+
)+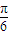 ],利用两角和的正弦公式求得结果.
],利用两角和的正弦公式求得结果.
解答:解:(I)因为函数f(x)=cos(2x-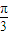 )+sin2x-cos2x=
)+sin2x-cos2x= cos2x+
cos2x+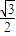 sin2x-cos2x
sin2x-cos2x
=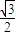 sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x-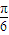 ),∴当 2kπ+
),∴当 2kπ+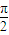 ≤x≤2kπ+
≤x≤2kπ+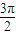 ,k∈z,
,k∈z,
即 kπ+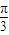 ≤x≤kπ+
≤x≤kπ+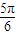 时,函数 f(x)递减.
时,函数 f(x)递减.
故,所求函数f(x)的减区间为[kπ+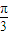 ≤x≤kπ+
≤x≤kπ+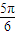 ],k∈z.
],k∈z.
(II)因为2a是第一象限角,且 sin(2a-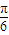 )=
)=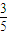 ,所以,2kπ-
,所以,2kπ-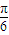 <2a-
<2a-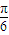 <2kπ+
<2kπ+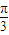 ,k∈z.
,k∈z.
由 f(a)=sin(2a-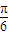 )=
)=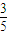 ,得cos(2a-
,得cos(2a-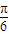 )=
)=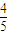 .所以,sin2a=sin[(2a-
.所以,sin2a=sin[(2a- )+
)+ ]=
]=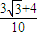 .
.
点评:本题考查三角函数性质及简单的三角变换,要求学生能正确运用三角函数的概念和公式对已知的三角函数进行化简求值.
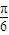 ),由2kπ+
),由2kπ+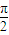 ≤x≤2kπ+
≤x≤2kπ+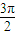 ,k∈z,求出
,k∈z,求出函数f(x)的减区间.
(II)根据sin(2a-
 )=
)=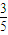 ,2kπ-
,2kπ-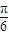 <2a-
<2a-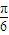 <2kπ+
<2kπ+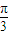 ,k∈z,利用同角三角函数的基本关系 求出cos(2a-
,k∈z,利用同角三角函数的基本关系 求出cos(2a-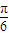 )
)的值,由sin2a=sin[(2a-
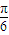 )+
)+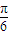 ],利用两角和的正弦公式求得结果.
],利用两角和的正弦公式求得结果.解答:解:(I)因为函数f(x)=cos(2x-
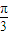 )+sin2x-cos2x=
)+sin2x-cos2x= cos2x+
cos2x+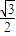 sin2x-cos2x
sin2x-cos2x =
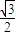 sin2x-
sin2x- cos2x=sin(2x-
cos2x=sin(2x-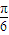 ),∴当 2kπ+
),∴当 2kπ+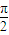 ≤x≤2kπ+
≤x≤2kπ+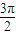 ,k∈z,
,k∈z,即 kπ+
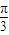 ≤x≤kπ+
≤x≤kπ+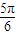 时,函数 f(x)递减.
时,函数 f(x)递减.故,所求函数f(x)的减区间为[kπ+
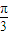 ≤x≤kπ+
≤x≤kπ+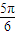 ],k∈z.
],k∈z.(II)因为2a是第一象限角,且 sin(2a-
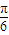 )=
)=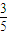 ,所以,2kπ-
,所以,2kπ-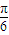 <2a-
<2a-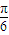 <2kπ+
<2kπ+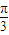 ,k∈z.
,k∈z.由 f(a)=sin(2a-
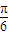 )=
)=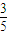 ,得cos(2a-
,得cos(2a-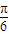 )=
)=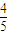 .所以,sin2a=sin[(2a-
.所以,sin2a=sin[(2a- )+
)+ ]=
]=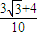 .
.点评:本题考查三角函数性质及简单的三角变换,要求学生能正确运用三角函数的概念和公式对已知的三角函数进行化简求值.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )