题目内容
2. 斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.
斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.(1)求证:平面ABC⊥平面ABC1;
(2)求BC与平面AA1C1C所成的角;
(3)求这个三棱柱的体积.
分析 (1)运用线面垂直的判定定理和面面垂直的判定定理,即可得证;
(2)设B到平面ACC1的距离为h,运用线面垂直的性质和等积法,求得h,求得线面所成角的正弦即可;
(3)将该三棱柱,补成一个四棱柱,三棱柱的体积为四棱柱的一半.计算即可得到.
解答  解:(1)证明:由题意AC⊥AB,AC⊥BC1,
解:(1)证明:由题意AC⊥AB,AC⊥BC1,
即有AC⊥平面ABC1,
AC?平面ABC,
则平面ABC⊥平面ABC1;
(2)设B到平面ACC1的距离为h,
由AC⊥平面ABC1,
可得侧棱CC1与平面ABC1成60°角,即为∠ACC1=60°,
在直角三角形ACC1中,AC1=6$\sqrt{3}$,CC1=12,
在△ABC1中,AB=6,BC1=2$\sqrt{6}$,AC1=6$\sqrt{3}$,
cos∠BAC1=$\frac{36+36×3-24}{2×6×6\sqrt{3}}$=$\frac{5}{3\sqrt{3}}$,
则${S}_{△AB{C}_{1}}$=$\frac{1}{2}$×6×6$\sqrt{3}$×$\frac{\sqrt{2}}{3\sqrt{3}}$=6$\sqrt{2}$,
由等积法,可得${V}_{B-AC{C}_{1}}$=${V}_{C-AB{C}_{1}}$,
即为$\frac{1}{3}$h•$\frac{1}{2}$•6•6$\sqrt{3}$=$\frac{1}{3}$•6•6$\sqrt{2}$,
解得h=$\frac{2\sqrt{2}}{\sqrt{3}}$,
即有BC与平面AA1C1C所成的角的正弦为$\frac{h}{BC}$=$\frac{2\sqrt{2}}{\sqrt{3}}$•$\frac{1}{6\sqrt{2}}$=$\frac{\sqrt{3}}{9}$.
则BC与平面AA1C1C所成的角为arcsin$\frac{\sqrt{3}}{9}$'
(3)将该三棱柱,补成一个四棱柱,如图.
则三棱柱的体积为四棱柱的一半.
即有体积为$\frac{1}{2}$h•${S}_{AC{C}_{1}{A}_{1}}$=$\frac{1}{2}$•$\frac{2\sqrt{2}}{\sqrt{3}}$•6•6$\sqrt{3}$=36$\sqrt{2}$.
点评 本题考查美梦成真的判定和线面所成角的求法、三棱柱的体积的求法,考查空间线面位置关系的运用,等积法,考查运算能力,属于中档题.

| A. | 1 | B. | $\frac{5}{6}$ | C. | 2 | D. | $\frac{4}{3}$ |
| A. | (1,3] | B. | (-∞,3] | C. | (0,3] | D. | (1,3) |
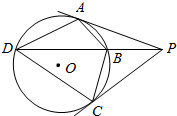 如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证:
如图所示,已知PBD是⊙O的割线,PA、PC是⊙O的切线,A、C为切点,求证: 已知:如图,点I是△ABC的内心,延长AI交△ABC的外接圆于点D,求证:点D是△BCI的外心.
已知:如图,点I是△ABC的内心,延长AI交△ABC的外接圆于点D,求证:点D是△BCI的外心.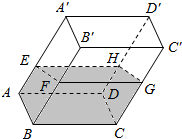 如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A′B′C′D′容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法: 如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.
如图,已知⊙O是△ABC的外接圆,AB=BC,AD是BC边上的高,AE是⊙O的直径.