题目内容
3.已知函数f(x)=$\sqrt{4-{a}^{x}}$(a>0且a≠1),则其值域为[0,2).分析 要使函数f(x)=$\sqrt{4-{a}^{x}}$(a>0且a≠1)有意义,可得4-ax≥0,又ax>0,可得4>4-ax≥0,即可得出.
解答 解:要使函数f(x)=$\sqrt{4-{a}^{x}}$(a>0且a≠1)有意义,
可得4-ax≥0,又ax>0,
∴4>4-ax≥0,
∴2$>\sqrt{4-{a}^{x}}$≥0,
其值域为:[0,2).
点评 本题考查了根式函数与指数函数的单调性、值域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在△ABC中,tanA是以-4为第4项、4为第8项的等差数列{an}的公差,tanB是以$\frac{1}{3}$为第2项、9为第5项的等比数列{bn}的公比,则△ABC是( )
| A. | 钝角三角形 | B. | 等腰直角三角形 | C. | 锐角三角形 | D. | 以上都不对 |
3.如图,已知∠DEC=80°,弧CD的度数与弧AB的度数的差为20°,则∠DAC的度数为( )


| A. | 35° | B. | 45° | C. | 55° | D. | 70° |
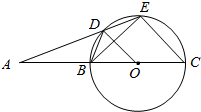 已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE.
已知圆O,点A为圆O外一点,BC为圆O的直径,过A作圆O的割线交圆O于D,E两点,其满足BD=DE. 斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.
斜三棱柱ABC-A1B1C1的两底面为等腰三角形,直角边AB=AC=6,BC1⊥AC,BC1=2$\sqrt{6}$,侧棱CC1与平面ABC1成60°角.