题目内容
下列命题:①若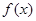 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,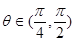 ,则
,则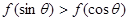 ;②若锐角
;②若锐角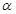 、
、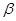 满足
满足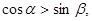 则
则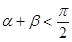 ; ③在
; ③在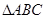 中,“
中,“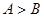 ”是“
”是“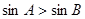 ”成立的充要条件;④要得到函数
”成立的充要条件;④要得到函数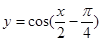 的图象,只需将
的图象,只需将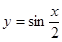 的图象向左平移
的图象向左平移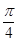 个单位.其中真命题的个数有( )
个单位.其中真命题的个数有( )
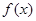 是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,
是定义在[-1,1]上的偶函数,且在[-1,0]上是增函数,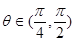 ,则
,则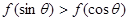 ;②若锐角
;②若锐角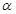 、
、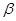 满足
满足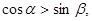 则
则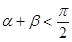 ; ③在
; ③在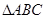 中,“
中,“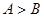 ”是“
”是“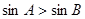 ”成立的充要条件;④要得到函数
”成立的充要条件;④要得到函数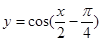 的图象,只需将
的图象,只需将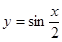 的图象向左平移
的图象向左平移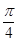 个单位.其中真命题的个数有( )
个单位.其中真命题的个数有( )| A.1 | B.2 | C.3 | D.4 |
B
因为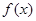 是定义在
是定义在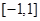 上的偶函数,且在
上的偶函数,且在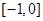 上单调增,所以
上单调增,所以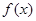 在
在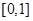 上单调减。因为
上单调减。因为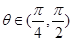 ,所以
,所以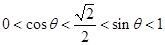 ,由单调性可得
,由单调性可得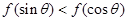 ,①不正确;
,①不正确;
若锐角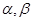 满足
满足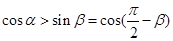 ,所以根据函数
,所以根据函数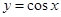 的单调性可得
的单调性可得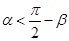 ,即
,即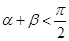 ,②正确;
,②正确;
若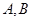 都是锐角,则由
都是锐角,则由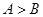 可得
可得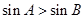 。若
。若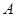 是钝角,则由
是钝角,则由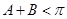 有
有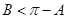 ,从而可得
,从而可得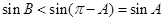 。所以由
。所以由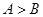 可得
可得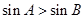 。反之,若
。反之,若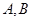 都是锐角,则由
都是锐角,则由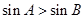 可得
可得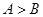 。若
。若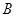 是钝角,则由
是钝角,则由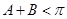 有
有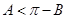 ,所以
,所以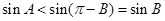 ,与
,与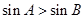 矛盾,所以不成立。若
矛盾,所以不成立。若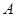 是钝角,由
是钝角,由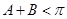 有
有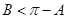 ,从而可得
,从而可得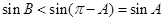 ,成立,此时有
,成立,此时有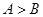 。所以由
。所以由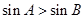 可得
可得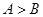 。所以“
。所以“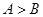 ”是“
”是“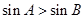 ”的充要条件,③正确;
”的充要条件,③正确;
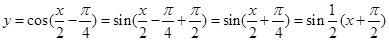 ,所以函数
,所以函数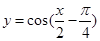 的图象可由函数
的图象可由函数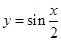 的图象向左平移
的图象向左平移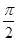 个单位得到,④不正确。
个单位得到,④不正确。
综上可得,选B
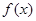 是定义在
是定义在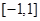 上的偶函数,且在
上的偶函数,且在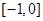 上单调增,所以
上单调增,所以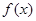 在
在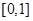 上单调减。因为
上单调减。因为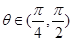 ,所以
,所以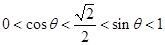 ,由单调性可得
,由单调性可得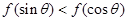 ,①不正确;
,①不正确;若锐角
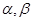 满足
满足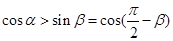 ,所以根据函数
,所以根据函数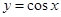 的单调性可得
的单调性可得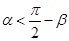 ,即
,即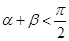 ,②正确;
,②正确;若
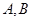 都是锐角,则由
都是锐角,则由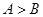 可得
可得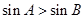 。若
。若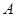 是钝角,则由
是钝角,则由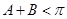 有
有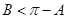 ,从而可得
,从而可得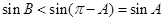 。所以由
。所以由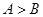 可得
可得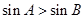 。反之,若
。反之,若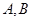 都是锐角,则由
都是锐角,则由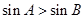 可得
可得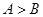 。若
。若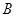 是钝角,则由
是钝角,则由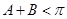 有
有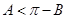 ,所以
,所以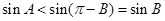 ,与
,与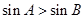 矛盾,所以不成立。若
矛盾,所以不成立。若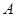 是钝角,由
是钝角,由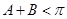 有
有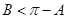 ,从而可得
,从而可得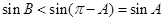 ,成立,此时有
,成立,此时有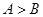 。所以由
。所以由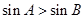 可得
可得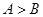 。所以“
。所以“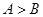 ”是“
”是“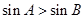 ”的充要条件,③正确;
”的充要条件,③正确;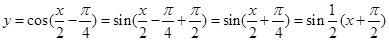 ,所以函数
,所以函数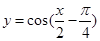 的图象可由函数
的图象可由函数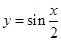 的图象向左平移
的图象向左平移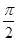 个单位得到,④不正确。
个单位得到,④不正确。综上可得,选B

练习册系列答案
相关题目
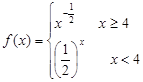 的单调减区间为( )
的单调减区间为( )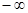 ,
,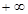 )
)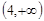
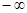 ,4)和
,4)和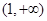 上单调递增的( )
上单调递增的( )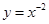
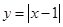
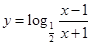
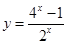
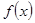 是偶函数,它在
是偶函数,它在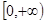 上是减函数,若
上是减函数,若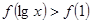 ,则
,则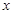 的取值范 围是( )
的取值范 围是( )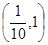
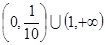
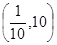
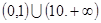
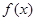 是定义在
是定义在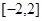 上增函数,且
上增函数,且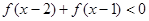 ,求x的取值范围.
,求x的取值范围.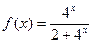 ,
,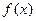 是R上的增函数;(6分)
是R上的增函数;(6分)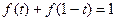 ;(4分)
;(4分)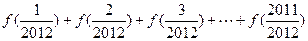 。(4分)
。(4分)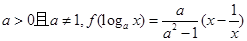 .
.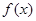 ;(2)判断
;(2)判断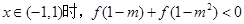 ,求m的集合M。
,求m的集合M。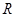 上的偶函数
上的偶函数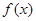 在区间
在区间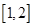 上是增函数。且满足
上是增函数。且满足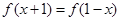 ,关于函数
,关于函数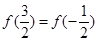 ; ②图像关于直线
; ②图像关于直线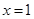 对称;
对称; 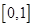 上是减函数;④在区间
上是减函数;④在区间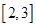 上是增函数;
上是增函数;