题目内容

设F1、F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，P是其右准线上纵坐标为
3
c（c为半焦距）的点，且|F1F2|=|F2P|，则椭圆的离心率是（　　）
A、
3
-1
2
B、
1
2
C、
5
-1
2
D、
2
2
分析：求离心率就寻找a，c的关系，借助与|F1F2|=|F2P|，Rt△PMF2建立等量关系求出离心率．
解答：解：
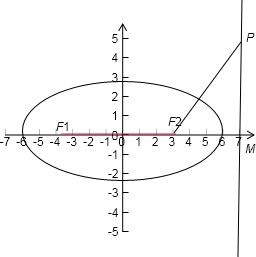精英家教网由已知P（
a2
c
，
3
c），
所以2c=
(
a2
c
-c)2+(
3
c)2
化简得a2-2c2=0?e=
c
a
=
2
2
，
故选D．
点评：本题考查了学生分析问题的能力，通过画图寻找a，c的关系，求解椭圆的离心率
练习册系列答案
相关题目
设F1，F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，若在直线x=
a2
c
上存在点P，使线段PF1的中垂线过点F2，则椭圆的离心率的取值范围是
（
3
3
，1）
（
3
3
，1）
．
设F1，F2分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左右焦点，若椭圆C上的一点A（1，
3
2
）到F1，F2的距离之和为4．
（1）求椭圆方程；
（2）若M，N是椭圆C上两个不同的点，线段MN的垂直平分线与x轴交于点P，求证：|
OP
|＜
1
2
；
（3）若M，N是椭圆C上两个不同的点，Q是椭圆C上不同于M，N的任意一点，若直线QM，QN的斜率分别为KQM•KQN．问：“点M，N关于原点对称”是KQM•KQN=-
3
4
的什么条件？证明你的结论．
（2009•南汇区二模）设F1、F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，其右焦点是直线y=x-1与x轴的交点，短轴的长是焦距的2倍．
（1）求椭圆的方程；
（2）若P是该椭圆上的一个动点，求
PF1
•
PF2
的最大值和最小值；
（3）是否存在过点A（5，0）的直线l与椭圆交于不同的两点C、D，使得|F2C|=|F2D|？若存在，求直线l的方程；若不存在，请说明理由．
（2013•安徽）设椭圆E：
x2
a2
+
y2
1-a2
=1的焦点在x轴上
（1）若椭圆E的焦距为1，求椭圆E的方程；
（2）设F1，F2分别是椭圆E的左、右焦点，P为椭圆E上第一象限内的点，直线F2P交y轴于点Q，并且F1P⊥F1Q，证明：当a变化时，点P在某定直线上．
（2009•南汇区二模）设F1、F2分别是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点，其右焦点是直线y=x-1与x轴的交点，短轴的长是焦距的2倍．
（1）求椭圆的方程；
（2）若P是该椭圆上的一个动点，求
PF1
•
PF2
的最大值和最小值；
（3）若P是该椭圆上的一个动点，点A（5，0），求线段AP中点M的轨迹方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网