��Ŀ����
��F1��F2�ֱ�����ԲC��
+
=1��a��b��0�������ҽ��㣬����ԲC�ϵ�һ��A��1��
����F1��F2�ľ���֮��Ϊ4��
��1������Բ���̣�
��2����M��N����ԲC��������ͬ�ĵ㣬�߶�MN�Ĵ�ֱƽ������x�ύ�ڵ�P����֤��|
|��
��
��3����M��N����ԲC��������ͬ�ĵ㣬Q����ԲC�ϲ�ͬ��M��N������һ�㣬��ֱ��QM��QN��б�ʷֱ�ΪKQM•KQN���ʣ�����M��N����ԭ��Գơ���KQM•KQN=-
��ʲô������֤����Ľ��ۣ�
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
��1������Բ���̣�
��2����M��N����ԲC��������ͬ�ĵ㣬�߶�MN�Ĵ�ֱƽ������x�ύ�ڵ�P����֤��|
| OP |
| 1 |
| 2 |
��3����M��N����ԲC��������ͬ�ĵ㣬Q����ԲC�ϲ�ͬ��M��N������һ�㣬��ֱ��QM��QN��б�ʷֱ�ΪKQM•KQN���ʣ�����M��N����ԭ��Գơ���KQM•KQN=-
| 3 |
| 4 |
��������1��������ɵ�
����ü��ɣ�
��2�������߶δ�ֱƽ���ߵ����ʺ͵�����Բ�ϼ��ɵó���
��3�����á���M��N����ԭ��Գơ���б�ʼ��㹫ʽ���ɵó���
|
��2�������߶δ�ֱƽ���ߵ����ʺ͵�����Բ�ϼ��ɵó���
��3�����á���M��N����ԭ��Գơ���б�ʼ��㹫ʽ���ɵó���
����⣺��1��������ɵ�
�����a=2��b2=3��
����Բ����Ϊ
+
=1��
��2����M��x1��y1����N��x2��y2����P��x0��0����
��|PM|=|PN|����(x1-x0)2+
=(x2-y2)2+
����*��
��M��N����Բ�ϣ���
=3-
��
=3-
��
���루*����x0=
��
=
������|
|��
��
��3������M��N����ԭ��Գơ���KQM•KQN=-
�ij�Ҫ������
֤������M��x1��y1����Q��x0��y0������N��-x1��-y1����
����
+
=1��
+
=1���õ�
=-
��
��kQM•kQN=
•
=
=-
?��M��N����ԭ��Գƣ�
|
����Բ����Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2����M��x1��y1����N��x2��y2����P��x0��0����
��|PM|=|PN|����(x1-x0)2+
| y | 2 1 |
| y | 2 2 |
��M��N����Բ�ϣ���
| y | 2 1 |
| 3 |
| 4 |
| x | 2 1 |
| y | 2 2 |
| 3 |
| 4 |
| x | 2 2 |
���루*����x0=
| x1+x2 |
| 8 |
| 2+2 |
| 8 |
| 1 |
| 2 |
| OP |
| 1 |
| 2 |
��3������M��N����ԭ��Գơ���KQM•KQN=-
| 3 |
| 4 |
֤������M��x1��y1����Q��x0��y0������N��-x1��-y1����
����
| ||
| 4 |
| ||
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||||
|
| 3 |
| 4 |
��kQM•kQN=
| y1-y0 |
| x1-x0 |
| -y1-y0 |
| -x1-x0 |
| ||||
|
| 3 |
| 4 |
����������������Բ�ı����̼������ʡ�б�ʼ��㹫ʽ����Ҫ�������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
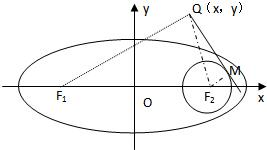 ��F1��F2�ֱ�����ԲC��
��F1��F2�ֱ�����ԲC��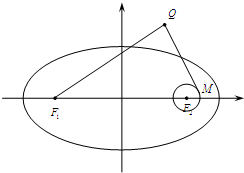 ��F1��F2�ֱ�����Բ
��F1��F2�ֱ�����Բ