题目内容
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 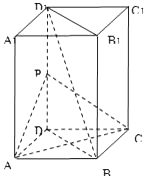
(1)求证:直线BD1∥平面PAC;
(2)求证:平面PAC⊥平面BDD1B1;
(3)求CP与平面BDD1B1所成的角大小.
【答案】
(1)证明:设AC和BD交于点O,连PO,由P,O分别是DD1,BD的中点,故PO∥BD1,
∵PO平面PAC,BD1平面PAC,所以,直线BD1∥平面PAC
(2)解:长方体ABCD﹣A1B1C1D1中,AB=AD=1,底面ABCD是正方形,则AC⊥BD,又DD1⊥面ABCD,则DD1⊥AC.
∵BD平面BDD1B1,D1D平面BDD1B1,BD∩D1D=D,∴AC⊥面BDD1B1.∵AC平面PAC,∴平面PAC⊥平面BDD1B1
(3)解:由(2)已证:AC⊥面BDD1B1,∴CP在平面BDD1B1内的射影为OP,∴∠CPO是CP与平面BDD1B1所成的角.
依题意得 ![]() ,
, ![]() ,在Rt△CPO中,
,在Rt△CPO中, ![]() ,∴∠CPO=30°
,∴∠CPO=30°
∴CP与平面BDD1B1所成的角为30°
【解析】(1)设AC和BD交于点O,由三角形的中位线的性质可得PO∥BD1 , 从而证明直线BD1∥平面PAC.(2)证明AC⊥BD,DD1⊥AC,可证AC⊥面BDD1B1 , 进而证得平面PAC⊥平面BDD1B1 . (3)CP在平面BDD1B1内的射影为OP,故∠CPO是CP与平面BDD1B1所成的角,在Rt△CPO中,利用边角关系求得∠CPO的大小.
【考点精析】通过灵活运用直线与平面平行的判定和平面与平面垂直的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直即可以解答此题.