题目内容
10.设a<0,记函数f(x)=a$\sqrt{1{-x}^{2}}$+$\sqrt{1+x}$+$\sqrt{1-x}$.设t=$\sqrt{1+x}$+$\sqrt{1-x}$,求t的取值范围,并把f(x)的最大值表示为t的函数m(t).分析 令t=$\sqrt{1+x}$+$\sqrt{1-x}$,由1+x≥0且1-x≥0,得-1≤x≤1,再由${t}^{2}=2+2\sqrt{1-{x}^{2}}∈[2,4]$,且t≥0…①,可得t的取值范围是[$\sqrt{2}$,2],进而得m(t)的解析式,直线t=-$\frac{1}{a}$是抛物线m(t)=$\frac{1}{2}$at2+t-a的对称轴,分类讨论,利用函数的单调性求出函数f(x)的最大值为g(a).
解答 解:∵t=$\sqrt{1+x}$+$\sqrt{1-x}$,∴要使t有意义,必须1+x≥0且1-x≥0,即-1≤x≤1.
∵${t}^{2}=2+2\sqrt{1-{x}^{2}}∈[2,4]$,且t≥0…①,∴t的取值范围是[$\sqrt{2}$,2].
由①得:$\sqrt{1-{x}^{2}}$=$\frac{1}{2}{t}^{2}-1$,
∴m(t)=$\frac{1}{2}$at2+t-a,t∈[$\sqrt{2}$,2].
直线t=-$\frac{1}{a}$是抛物线m(t)=$\frac{1}{2}$at2+t-a的对称轴
当a<0时,函数y=m(t)(t∈[$\sqrt{2}$,2])的图象是开口向下的抛物线的一段,
若t=-$\frac{1}{a}$∈(0,$\sqrt{2}$]即a≤-$\frac{\sqrt{2}}{2}$时,g(a)=m($\sqrt{2}$)=$\sqrt{2}$,
若t=-$\frac{1}{a}$∈($\sqrt{2}$,2]即a∈(-$\frac{\sqrt{2}}{2}$,-$\frac{1}{2}$]时,g(a)=m(-$\frac{1}{a}$)=-a-$\frac{1}{2a}$,
若t=-$\frac{1}{a}$∈(2,+∞)即a∈(-$\frac{1}{2}$,0)时,g(a)=m(2)=a+2.
综上所述,有g(a)=$\left\{\begin{array}{l}{a+2,a>-\frac{1}{2}}\\{-a-\frac{1}{2a},-\frac{\sqrt{2}}{2}<a≤-\frac{1}{2}}\\{\sqrt{2},a≤-\frac{\sqrt{2}}{2}}\end{array}\right.$.
点评 本题考查函数的最值,考查换元法,考查分类讨论的数学思想,正确换元是关键.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案在一次篮球定点投篮训练中,规定每人最多投3次,在 处每投进一球得3分;在
处每投进一球得3分;在 处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在
处每投进一球得2分.如果前两次得分之和超过3分就停止投篮;否则投第三次.某同学在 处的投中率
处的投中率 ,在
,在 处的投中率为
处的投中率为 ,该同学选择先在
,该同学选择先在 处投第一球,以后都在
处投第一球,以后都在 处投,且每次投篮都互不影响,用
处投,且每次投篮都互不影响,用 表示该同学投篮训练结束后所得的总分,其分布列为:
表示该同学投篮训练结束后所得的总分,其分布列为:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求 的值;
的值;
(2)求随机变量 的数学期望
的数学期望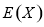 ;
;
(3)试比较该同学选择上述方式投篮得分超过3分与选择都在 处投篮得分超过3分的概率的大小.
处投篮得分超过3分的概率的大小.
| A. | (1,0) | B. | (0,1) | C. | (2,0) | D. | (0,2) |
 ,则
,则 ________
________  __________.
__________.





