题目内容
15.已知函数f(x)=2x+$\frac{4}{x}$-1,求f(x)的极值.分析 由题意求导f′(x),从而可确定f(x)的单调性,再求极值即可.
解答 解:∵函数f(x)=2x+$\frac{4}{x}$-1,
∴f′(x)=2-$\frac{4}{{x}^{2}}$=$\frac{{2x}^{2}-4}{{x}^{2}}$;
故当x∈(-∞,-$\sqrt{2}$),($\sqrt{2}$,+∞)时,f′(x)>0;
当x∈(-$\sqrt{2}$,0),(0,$\sqrt{2}$)时,f′(x)<0;
故f(x)在(-∞,-$\sqrt{2}$),($\sqrt{2}$,+∞)上是增函数,
在(-$\sqrt{2}$,0),(0,$\sqrt{2}$)上是减函数;
故f极小值(x)=f($\sqrt{2}$)=4$\sqrt{2}-1$
f极大值(x)=f(-$\sqrt{2}$)=$-4\sqrt{2}-1$.
点评 本题考查了导数的综合应用,属于中档题,函数的极值的求法,考查计算能力.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
20.过抛物线C1:y=ax2(a>0)的焦点作y轴的垂线交抛物线C1于A,B两点,若△OAB(O是坐标原点)是面积为$\frac{1}{2}$的等腰三角形,则a的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 的前
的前 项和为
项和为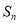 ,若
,若 ,且
,且 ,则
,则 等于( )
等于( )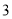 B.
B.  C.
C.  D.
D. 
 ,
, ,
, ,则输出的结果是( )
,则输出的结果是( )
 B.
B. C.
C. D.
D.
 满足条件
满足条件 ,且
,且 的最小值为6,
的最小值为6, ,则
,则 ___________.
___________.