题目内容
19.是否存在经过互异三点(1,1)、(3,2)和(m,1)的抛物线y=ax2+bx+c?若存在,求a、b、c的值;若不存在,请说明理由.分析 根据题意得出$\left\{\begin{array}{l}{a+b+c=1}\\{9a+3b+c=2}\\{a{m}^{2}+bm+c=1}\end{array}\right.$,$-\frac{b}{2a}$=$\frac{m+1}{2}$,化简求即可得出a=$\frac{1}{2}$,b=$-\frac{3}{2}$,c=2,m=1,利用m≠1,可判断.
解答 解:∵经过互异三点(1,1)、(3,2)和(m,1)的抛物线y=ax2+bx+c,
∴$\left\{\begin{array}{l}{a+b+c=1}\\{9a+3b+c=2}\\{a{m}^{2}+bm+c=1}\end{array}\right.$
根据对称得出:$-\frac{b}{2a}$=$\frac{m+1}{2}$,
化简得出:b=-a(m+1),a=$\frac{1}{6-2m}$,b=$\frac{m+1}{2m-6}$,=$\frac{m-6}{2m-6}$,
∴m=3,不存在
当m≠1(m=1三点互异)且m≠3时存在
.
点评 本题考查了二次函数的解析式的运用转化为方程组方法求解,计算难度较大,需仔细认真.

练习册系列答案
相关题目
14.若x,y满足$\left\{\begin{array}{l}kx+y≤4\\ 2y-x≤4\\ x≥0\\ y≥0\end{array}\right.$,且z=5y-x的最小值为-8,则k的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
6.已知(1+$\frac{2}{i}$)2=a+bi(a,b∈R,i为虚数单位),则a+b=( )
| A. | -7 | B. | 7 | C. | C-4 | D. | 4 |
 的前
的前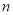 项和为
项和为 ,若
,若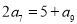 ,则
,则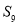 的值为( )
的值为( )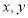 满足条件
满足条件 ,且
,且 的最小值为6,
的最小值为6,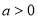 ,则
,则 ___________.
___________.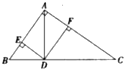 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB与E.求证
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DF⊥AC于F,DE⊥AB与E.求证