题目内容
2.设函数f(x)=$co{s}^{2}(\frac{π}{2}+x)$+$\sqrt{3}$sin($\frac{π}{2}$+x)cos($\frac{5π}{2}$-x),x∈R,求函数f(x)的单调递增区间,并求f(x)在区间[-$\frac{π}{4},\frac{π}{6}$]上的最小值.分析 由三角函数中的恒等变换应用化简函数解析式可得:f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,由2k$π-\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解函数f(x)的单调递增区间.由x∈[-$\frac{π}{4},\frac{π}{6}$],得2x-$\frac{π}{6}$∈[-$\frac{2π}{3}$,$\frac{π}{6}$],从而解得f(x)∈[-$\frac{1}{2}$,1],即可求得f(x)在区间[-$\frac{π}{4},\frac{π}{6}$]上的最小值.
解答 解:∵f(x)=$co{s}^{2}(\frac{π}{2}+x)$+$\sqrt{3}$sin($\frac{π}{2}$+x)cos($\frac{5π}{2}$-x)
=sin2x+$\sqrt{3}$cosxsinx
=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x
=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$,
∴由2k$π-\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z可解得:kπ$-\frac{π}{6}$≤x≤kπ+$\frac{π}{3}$,k∈Z,
故函数f(x)的单调递增区间是:[kπ$-\frac{π}{6}$,kπ+$\frac{π}{3}$],k∈Z,
∵x∈[-$\frac{π}{4},\frac{π}{6}$],
∴2x-$\frac{π}{6}$∈[-$\frac{2π}{3}$,$\frac{π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈[-1,$\frac{1}{2}$],f(x)=sin(2x-$\frac{π}{6}$)+$\frac{1}{2}$∈[-$\frac{1}{2}$,1]
∴f(x)在区间[-$\frac{π}{4},\frac{π}{6}$]上的最小值是:-$\frac{1}{2}$.
点评 本题主要考查了三角函数中的恒等变换应用,考查了三角函数的图象与性质,解题时注意讨论角的范围,属于基本知识的考查.

| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
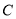 :
: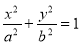 (
( )的短轴长为
)的短轴长为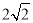 ,点
,点 在C上,平行于OM的直线
在C上,平行于OM的直线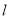 交椭圆C于不同的两点A,B.
交椭圆C于不同的两点A,B.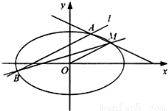
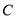 的方程;
的方程; 轴总围成等腰三角形.
轴总围成等腰三角形. 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点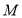 的极坐标为
的极坐标为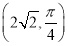 ,曲线
,曲线 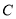 的参数方程为
的参数方程为 (
(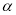 为参数).
为参数).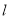 过
过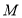 且与曲线
且与曲线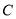 相切,求直线
相切,求直线 的极坐标方程;
的极坐标方程;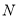 与点
与点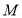 关于
关于 轴对称,求曲线
轴对称,求曲线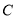 上的点到点
上的点到点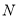 的距离的取值范围.
的距离的取值范围.