题目内容
若不等式 对
对 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 .
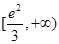
解析试题分析:由 得
得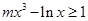 或
或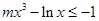 ,即
,即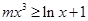 或
或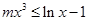 .又
.又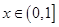 ,所以
,所以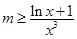 或
或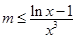 .因为不等式
.因为不等式 对
对 恒成立,所以
恒成立,所以 或
或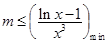 .(1)令
.(1)令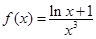 ,则
,则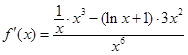
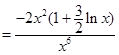 .令
.令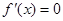 得
得 ,当
,当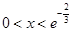 时,
时, ;当
;当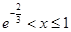 时,
时,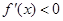 .所以
.所以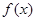 在
在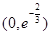 上是增函数,在
上是增函数,在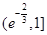 是减函数.所以
是减函数.所以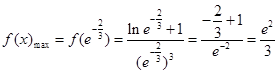 ,所以
,所以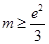 .(2)令
.(2)令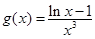 ,则
,则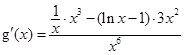
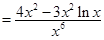 ,因为
,因为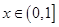 ,所以
,所以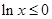 ,所以易知
,所以易知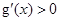 ,所以
,所以 在
在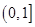 上是增函数.易知当
上是增函数.易知当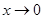 时,
时,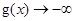 ,故
,故 在
在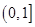 上无最小值,所以
上无最小值,所以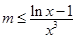 在
在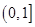 上不能恒成立.综上所述,
上不能恒成立.综上所述,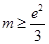 ,即实数
,即实数 的取值范围是
的取值范围是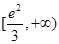 .
.
考点:利用导数研究函数的单调性、利用函数单调性求最值、含绝对值不等式的解法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
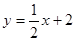 ,则
,则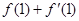 =______
=______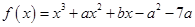 在
在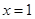 处取得极大值
处取得极大值 ,则
,则 的值为 .
的值为 .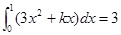 ,则
,则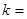 ________.
________. .
. 在点P处的切线平行于直线3x-y=0,则点P的坐标为 .
在点P处的切线平行于直线3x-y=0,则点P的坐标为 . 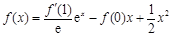 在点
在点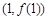 处的切线方程为_________.
处的切线方程为_________.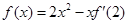 ,则函数
,则函数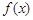 的图象在点
的图象在点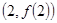 处的切线方程是 .
处的切线方程是 .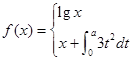
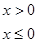 ,若
,若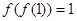 ,则
,则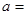 .
.