题目内容
设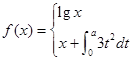
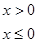 ,若
,若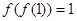 ,则
,则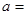 .
.
1
解析试题分析:因为,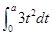 =
=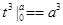 ,所以,
,所以,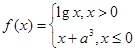 。
。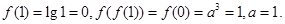
考点:定积分计算,分段函数,对数函数的性质。
点评:小综合题,本题思路清晰,通过计算定积分确定得到函数的解析式,进一步计算函数值。

练习册系列答案
相关题目
题目内容
设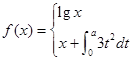
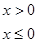 ,若
,若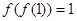 ,则
,则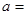 .
.
1
解析试题分析:因为,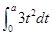 =
=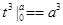 ,所以,
,所以,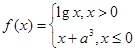 。
。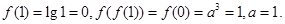
考点:定积分计算,分段函数,对数函数的性质。
点评:小综合题,本题思路清晰,通过计算定积分确定得到函数的解析式,进一步计算函数值。
